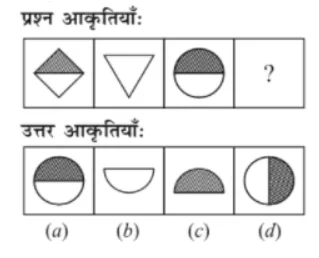
2, 3, 10, 38, 172 Find out the wrong number in the series.
2, 3, 10, 38, 172 श्रृंखला में गलत संख्या ज्ञात कीजिए।
2, 3, 10, 38, 172
2 × 1 + 12 = 3,
3 × 2 + 22 =10,
10 × 3 + 32 = 39,
39 × 4 + 42 = 172
Hence 38 is the wrong number and in place of 38, it should be 39. So the correct answer is option A.
2, 3, 10, 38, 172
2 × 1 + 12 = 3,
3 × 2 + 22 =10,
10 × 3 + 32 = 39,
39 × 4 + 42 = 172
अत: 38 गलत संख्या है और 38 के स्थान पर 39 होनी चाहिए। इसलिए सही उत्तर विकल्प A है।
In the given question, select the related number from the given alternatives.
24 : 126 : : 48 : ?
दिए गए प्रश्न में, दिए गए विकल्पों में से संबंधित संख्या का चयन करें।
24 : 126 : : 48 : ?
Relationship between 24:126-
5^2 – 1 = 24 ;
5^3 + 1 = 126
Similarly the relationship between 48:?-
7^2 – 1 = 48;
7^3 + 1 = 344
So the related number is 344.
Hence the correct answer is option C.
24:126 के बीच संबंध -
5^2 - 1 = 24
5^3 + 1 = 126
इसी प्रकार 48:? के बीच संबंध -
7^2 - 1 = 48;
7^3 + 1 = 344
संबंधित संख्या 344 है।
अतः सही उत्तर विकल्प C है।

On 8th Dec 2007, Saturday falls. What day of the week was it on 8th Dec 2006?
8 दिसंबर 2007 को शनिवार पड़ता है। 8 दिसंबर, 2006 को सप्ताह का कौन सा दिन था?
If day of same date is asked for next year and if next coming year is ordinary year then we add +1 because ordinary year has 1 odd day and if next coming year is leap year so we add +2 because there are 2 odd days in a leap year.
The year 2006 is an ordinary year. So, it has 1 odd day.
So, the day on 8th Dec, 2007 will be 1 day beyond the day on 8th Dec, 2006.
8th Dec, 2007 is Saturday.
Hence 8th Dec, 2006 is Friday. (Saturday-1)
So the correct answer is option D.
यदि एक ही तारीख का दिन अगले वर्ष के लिए पूछा जाता है और यदि अगला आने वाला वर्ष साधारण वर्ष है तो दिए हुए दिन में +1 कर दिया जाता है क्योंकि साधारण वर्ष में 1 विषम दिन होता है और यदि अगला आने वाला वर्ष लीप वर्ष है तो दिए हुए दिन में +2 कर दिया जाता है क्योंकि लीप वर्ष में 2 विषम दिन होते है l
वर्ष 2006 एक सामान्य वर्ष है। तो, इसमें 1 विषम दिन है।
तो, 8 दिसंबर, 2007 का दिन 8 दिसंबर, 2006 के दिन से 1 दिन आगे होगा।
8 दिसंबर 2007 को शनिवार है।
अतः 8 दिसंबर 2006 को शुक्रवार है। (शनिवार - 1)
इसलिए सही उत्तर विकल्प D है।
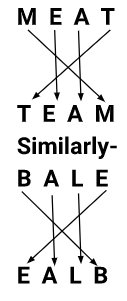
If MEAT is written as TEAM, how will BALE be written?
यदि MEAT को TEAM के रूप में लिखा जाता है तो BALE कैसे लिखा जायेगा ?
BALE will be written as EALB.
Hence the correct answer is option B.
You can see the solution in the below image -
BALE को EALB लिखा जाएगा।
अतः सही उत्तर विकल्प B है।
इसका समाधान आप नीचे चित्र में देख सकते हैं -
In which of the following years was the Second Round Table Conference in London held?
निम्नलिखित में से किस वर्ष लंदन में द्वितीय गोलमेज सम्मेलन आयोजित किया गया था?
The Second Round Table Conference was held in London from 7 September 1931 to 1 December 1931.
The Three Round Table Conferences of 1930–1932 were a series of peace conferences organized by the British government and Indian political figures to discuss constitutional reforms in India. These began in November 1930 and ended in December 1932.
The First Round Table Conference was formally inaugurated by George V at the Royal Gallery House of Lords in London on 12 November 1930 and was presided over by the Prime Minister.
An agreement between Mahatma Gandhi and the Viceroy Lord Irwin brought the Congress to the second session of the Round Table Conference, which was held on 7 September.
The third and last session was held on November 17, 1932.
So the correct answer is option A.
दूसरा गोलमेज सम्मेलन 7 सितंबर 1931 से 1 दिसंबर 1931 तक लंदन में आयोजित किया गया था।
1930-1932 के तीन गोलमेज सम्मेलन भारत में संवैधानिक सुधारों पर चर्चा करने के लिए ब्रिटिश सरकार और भारतीय राजनीतिक हस्तियों द्वारा आयोजित शांति सम्मेलनों की एक श्रृंखला थी। ये नवंबर 1930 में शुरू हुए और दिसंबर 1932 में समाप्त हुए।
प्रथम गोलमेज सम्मेलन का औपचारिक उद्घाटन जॉर्ज पंचम द्वारा 12 नवंबर 1930 को लंदन में रॉयल गैलरी हाउस ऑफ लॉर्ड्स में किया गया था और इसकी अध्यक्षता प्रधान मंत्री ने की थी।
महात्मा गांधी और वायसराय लॉर्ड इरविन के बीच एक समझौते ने कांग्रेस को गोलमेज सम्मेलन के दूसरे सत्र में लाया, जो 7 सितंबर को आयोजित किया गया था।
तीसरा और अंतिम सत्र 17 नवंबर, 1932 को आयोजित किया गया था।
इसलिए सही उत्तर विकल्प A है।
In the question, a sequence is given with one term missing. Select the option from the given options.
BEAG, DGCI, FIEK,?
प्रश्न में एक अनुक्रम दिया गया है जिसमे एक पद लुप्त है l दिए गये विकल्पों में से वह विकल्प चुनिए l
BEAG, DGCI,FIEK,?
B+2=D, D+2=F, F+2 = H
E+2=G, G+2=I, I+2=K
A+2=C, C+2=E, E+2=G
G+2=I, I+2=K, K+2=M
The missing term is HKGM.
Hence the correct answer is option D.
B+2=D, D+2=F, F+2 = H
E+2=G, G+2=I, I+2=K
A+2=C, C+2=E, E+2=G
G+2=I, I+2=K, K+2=M
अतः विलुप्त पद HKGM है l
इसलिए सही उत्तर विकल्प D है l
Four words have been given, out of which three are alike in some manner and one is different. Select the word that is different.
चार शब्द दिए गए हैं, जिनमें से तीन किसी तरह से एक जैसे हैं और एक अलग है। उस शब्द का चयन करें जो भिन्न है।
Intelligence, Aptitude, and Memory are the same meaning. But Weight is different from others.
So the correct answer is option B.
Intelligence, Aptitude और Memory तीनो का अर्थ में एक समान ही हैं। लेकिन Weight इनसे अलग है।
इसलिए सही उत्तर विकल्प B है।
Select the related word/letters/number from the given alternatives.
FILM:ADGH::MILK:?
दिए गए विकल्पों में से संबंधित शब्द/अक्षरों/संख्या को चुनिए।
FILM:ADGH::MILK:?
In the FILM:ADGH -
F-5=A
I-5=D
L-5=G
M-5=H
Similarly in MILK -
M-5=H
I-5=D
L-5=G
K-5=F
So the correct answer is option B.
FILM:ADGH में -
F-5=A
I-5=D
L-5=G
M-5=H
इसी प्रकार MILK में -
M-5=H
I-5=D
L-5=G
K-5=F
अतः सही उत्तर विकल्प A है l
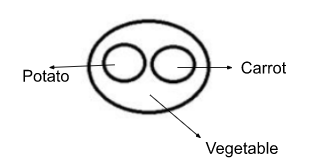
Select the Venn diagram that best illustrates the relationship between the following classes.
Potato, Vegetable, Carrot
वेन आरेख का चयन करें जो निम्नलिखित वर्गों के बीच के संबंध को सर्वोत्तम रूप से दर्शाता है।
आलू, सब्जी, गाजर
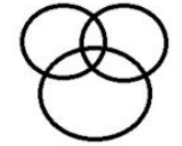
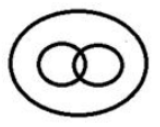
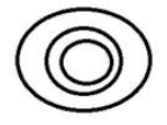
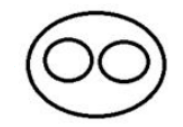
Potato and Carrots both are in the category of vegetables. Hence option D is the correct Venn diagram.
So the correct answer is option D.
आलू और गाजर दोनों ही सब्जी की श्रेणी में आते हैं। अत: विकल्प D सही वेन आरेख है।
इसलिए सही उत्तर विकल्प D है।
In a certain coding system, 'Read this book' is coded as '689', 'This book is useful' is coded as '9675', 'Useful book is good' is coded as '5479'. What is the code for 'This book is good' in this system?
एक निश्चित कूट प्रणाली में, 'Read this book' को '689' के रूप में कूटबद्ध किया जाता है, 'This book is useful' को '9675' के रूप में कूटबद्ध किया जाता है, 'Useful book is good' को '5479' के रूप में कूटबद्ध किया जाता है। इस कूट प्रणाली में 'This book is good' के लिए क्या कोड होगा?
Read this book = 6 8 9
This book is useful = 9 6 7 5
Useful book is good = 5 4 7 9
Code for ‘this’ = 6
Code for ‘book’ = 9
Code for ‘good’ = 4
Code for ‘is’ is either 5 or 7 but according to the option, only option C has code 496, so code for ‘is’ is 5.
Hence the code for -
‘This book is good’ = 4965
So the correct answer is option C.
Read this book = 6 8 9
This book is useful = 9 6 7 5
Useful book is good = 5 4 7 9
‘this’ के लिए कोड = 6
‘book’ के लिए कोड = 9
‘good’ के लिए कोड = 4
'is' के लिए कोड या तो 5 या 7 है लेकिन विकल्प के अनुसार, केवल विकल्प C में कोड 496 है, इसलिए 'is' के लिए कोड 5 है।
अतः ‘This book is good’ के लिए कोड = 4965
इसलिए सही उत्तर विकल्प C है।
In the question, a sequence is given with one term missing. Select the option from the given options.
16 25 9
36 64 81
10 13 ?
प्रश्न में एक अनुक्रम दिया गया है जिसमे एक पद लुप्त है l दिए गये विकल्पों में से वह विकल्प चुनिए l
16 25 9
36 64 81
10 13 ?
The sum of the square roots of the first two terms in each row is equal to the third number.
√16+√36 = 4+6=10
√25+√64=5+8=13
√9+√81=3+9=12
So the missing term is 12.
Hence the correct answer is option A.
प्रत्येक पंक्ति के प्रथम दो पदों के वर्गमूल का योग तीसरी संख्या के बराबर है l
√16+√36 = 4+6=10
√25+√64=5+8=13
√9+√81=3+9=12
अतः लुप्त संख्या 12 है l
इसलिए सही उत्तर विकल्प A है l
A does half as much work as B in three-fourths of the time. If they take 18 days to complete the work together, how much time shall B take to do it?
A, तीन-चौथाई समय में B से आधा कार्य करता है। यदि वे एक साथ कार्य को पूरा करने में 18 दिन लेते हैं, तो B उस कार्य को पूरा करने में कितना समय लेगा?
Given -
A does half as much work as B three-fourths of the time.
A*½ = B*¾
A = 3B/2
So A can do a work in 3B/2 days
1 day work of A = 1/3B/2 = 2/3B
1-day work of B = 1/B
A and B together can do the work in 18 days.
1-day work of A + B = 1/18
Then -
1-day work of A+B = 1-day work of A + 1-day work of B
1/18 = 2/3B+1/B
1/18 = 2+3/3B
1/18 = 5/3B
B = 18*5/3
B = 30 days
Hence B will take 30 days to the work.
So the correct answer is option A.
दिया गया है -
A, तीन-चौथाई समय में B से आधा कार्य करता है।
A*½ = B*¾
A = 3B/2
अत: A एक कार्य को 3B/2 दिनों में कर सकता है
A का 1 दिन का कार्य = 1/3B/2 = 2/3B
B का 1 दिन का कार्य = 1/B
A और B मिलकर उस काम को 18 दिनों में कर सकते हैं।
A+B का 1 दिन का कार्य = 1/18
तब -
A+B का 1 दिन का कार्य = A का 1 दिन का कार्य + B का 1 दिन का कार्य
1/18 = 2/3B+1/B
1/18 = 2+3/3B
1/18 = 5/3B
B = 18*5/3
B = 30 दिन
अत: B को कार्य करने में 30 दिन लगेंगे।
इसलिए सही उत्तर विकल्प A है।
Two pipes A and B can fill a tank in 15 min and 20 min, respectively. Both the pipes are opened together. But, after 4 min, pipe A is turned off. What is the total time required to fill the tank?
दो पाइप A और B क्रमशः 15 मिनट और 20 मिनट में एक टैंक भर सकते हैं। दोनों पाइप एक साथ खोले जाते हैं। लेकिन, 4 मिनट के बाद, पाइप A को बंद कर दिया जाता है। टैंक को भरने के लिए कुल समय क्या आवश्यक है?
Two pipes A and B can fill a tank in 15 min and 20 min.
The part filled by both the pipes A and B in 1 min = 1/15+1/20
= 4+3/60
=7/60
After 4 min, pipe A is turned off.
The part filled by both the pipe A and B in 4 min = 4*7/60 = 7/15
Remaining part = 1-7/15
= 15-7/15
= 8/15
The remaining part will be filled by pipe B.
Pipe B can fill the tank in 20 min.
So 8/15 part of the tank will be filled by pipe B = 20*8/15
= 32/3 min
= 10 ⅔ min
= 10 min 40 sec
So the total time to fill the tank = 4 min +10 min 40 sec = 14 min 40 sec
Hence the correct answer is option D.
दो पाइप A और B, 15 मिनट और 20 मिनट में एक टैंक भर सकते हैं।
1 मिनट में दोनों पाइप A और B द्वारा भरा हुआ भाग = 1/15+1/20
= 4+3/60
= 7/60
4 मिनट के बाद, पाइप A को बंद कर दिया जाता है।
4 मिनट में पाइप A और B दोनों द्वारा भरा हुआ भाग = 4*7/60 = 7/15
शेष भाग = 1-7/15
= 15-7/15
= 8/15
शेष भाग पाइप B द्वारा भरा जाएगा।
पाइप B, 20 मिनट में टैंक को भर सकता है।
तो पाइप B द्वारा टैंक का 8/15 भाग भरा जाएगा= 20*8/15 मिनट
= 32/3 मिनट
= 10 ⅔ मिनट
= 10 मिनट 40 सेकंड
तो टैंक को भरने का कुल समय = 4 मिनट +10 मिनट 40 सेकंड = 14 मिनट 40 सेकंड
अतः सही उत्तर विकल्प D है।
Pipe A can fill a tank in 16 minutes and pipe B can empty it in 24 minutes. If both the pipes are opened together after how many minutes should pipe B be closed, so that the tank is filled in 30 minutes?
पाइप A एक टैंक को 16 मिनट में भर सकता है और पाइप B इसे 24 मिनट में खाली कर सकता है। यदि दोनों पाइपों को एक साथ खोला जाता है, तो कितने मिनट बाद पाइप B को बंद कर देना चाहिए, ताकि टैंक 30 मिनट में भर जाए?
Pipe A can fill the tank in 16 min.
The part of the tank filled by pipe A in 1 min=1/16
Pipe B can fill the tank in 24 min.
The part of the tank filled by pipe B in 1 min = 1/24
According to the question pipe A work for whole time 30 min and pipe B work for 30-x min. It means after 30-x minutes the pipe B is closed.
The part of the tank filled by pipe A in 30 min =30/16 = 15/8
The part of the tank filled by pipe B in 30-x min = (30-x)/24
The part of the tank filled by pipe A in 30 min + The part of the tank filled by pipe B in 30-x min = 1 work
15/8+(30-x)/24 = 1
15/8-1=(30-x)/24
15-8/8 = (30-x)/24
⅞=(30-x)/24
7=30-x/3
21=30-x
x=30-21
x =9 min
After 30-x minutes the pipe B is closed = 30-9=21 min.
Hence after 21 the pipe B is closed.
Hence the correct answer is option C.
पाइप A टंकी को 16 मिनट में भर सकता है।
पाइप A द्वारा 1 मिनट में भरा गया टैंक का भाग = 1/16
पाइप B टंकी को 24 मिनट में भर सकता है।
पाइप B द्वारा 1 मिनट में भरा गया टैंक का भाग = 1/24
प्रश्न के अनुसार पाइप A पूरे समय = 30 मिनट के लिए काम करता है और पाइप B (30-x) मिनट के लिए काम करता है। इसका मतलब है कि 30-x मिनट के बाद पाइप B बंद हो जाता है।
पाइप A द्वारा 30 मिनट में भरा गया टैंक का भाग =30/16 = 15/8
पाइप B द्वारा 30-x मिनट में भरा गया टैंक का भाग = (30-x)/24
पाइप A द्वारा 30 मिनट में भरा गया टैंक का भाग + पाइप B द्वारा 30-x मिनट में भरा गया टैंक का भाग = 1 कार्य
15/8+(30-x)/24 = 1
15/8-1=(30-x)/24
15-8/8 = (30-x)/24
⅞=(30-x)/24
7=30-x/3
21=30-x
x=30-21
x =9 मिनट
पाइप B, 30-x = 30-9=21 मिनट के बाद बंद हो जाता है l
अतः 21 मिनट के बाद पाइप B को बंद कर दिया जाता है।
अतः सही उत्तर विकल्प C है।
A can do a work in 15 days and B in 20 days if they work on it together for 4 days then the fraction of the work that is left is?
A एक काम को 15 दिनों में और B 20 दिनों में कर सकता है यदि वे एक साथ 4 दिनों के लिए उस पर काम करते हैं तो शेष कार्य का अंश है ?
A can do a work in 15 days. Then -
1-day work of A = 1/15
B can do a work in 20 days. Then -
1-day work of B = 1/20
1 day work of A and B = 1/15 + 1/20 = 4+3/60 = 7/60
4 days work of for A and B = 4*7/60 = 7/15
Hence the fraction of work left = 1-1/15 = 8/15
So the correct answer is option D.
A एक काम को 15 दिनों में कर सकता है। तब -
A का 1 दिन का कार्य = 1/15
B एक काम को 20 दिनों में कर सकता है। तब -
B का 1 दिन का कार्य = 1/20
A और B का 1 दिन का कार्य = 1/15 + 1/20 = 4+3/60 = 7/60
A और B का 4 दिन का कार्य = 4*7/60 = 7/15
अत: शेष कार्य का अंश = 1-1/15 = 8/15
इसलिए सही उत्तर विकल्प D है।
The following data gives the results of a sample survey of three categories A, B, and C:
The percentage of elements in this sample belonging to the category B is:
निम्नलिखित आंकड़े तीन वर्गों A, B तथा C के लिए किए गए प्रतिदर्श सर्वेक्षण के परिणाम है:
इस प्रतिदर्श में वर्ग B से सम्बद्ध अवयवों का प्रतिशत है:

Total elements in the sample = 30
Total elements belonging to category B in this sample = 6
Percentage of elements belonging to category B in the sample = (Total elements belonging to category B / Total elements in the sample) * 100
= (6/30)*100
= 100/5
= 20%
Hence, the percentage of elements belonging to category B in this sample is 20%.
So the correct answer is option B.
प्रतिदर्श में कुल अवयव = 30
इस प्रतिदर्श में वर्ग B से सम्बद्ध कुल अवयव = 6
प्रतिदर्श में वर्ग B से सम्बद्ध अवयवों का प्रतिशत = (B से सम्बद्ध कुल अवयव/प्रतिदर्श में कुल अवयव)*100
= (6/30)*100
= 100/5
= 20%
अतः इस प्रतिदर्श में वर्ग B से सम्बद्ध अवयवों का प्रतिशत 20 % है।
इसलिए सही उत्तर विकल्प B है।
Protein factory in human cells is ?
मानव कोशिका में प्रोटीन फैक्टरी कौन-सी है?
Hence the correct answer is option A.
अतः सही उत्तर विकल्प A है l
In which disease blood clot is not formed?
किस रोग में रक्त का थक्का नहीं बनता है?
Thalassemia
Hence the correct answer is option C.
थेलेसीमिया
अतः सही उत्तर विकल्प C है l