Divide 1056 by 23 and we find if we add 2 to 1056 then it will be 1058 which is completely divided by 23. So the correct answer is option A.

1056 को 23 से विभाजित करें और हम पाते हैं कि यदि हम 1056 में 2 जोड़ते हैं तो यह 1058 होगा जो 23 से पूरी तरह से विभाजित है। इसलिए सही उत्तर विकल्प A है।

Let the two numbers= x,y the difference of two numbers is 1365. x-y=1365----(1) On dividing the larger number by the smaller, we get 6 as quotient and the 15 as remainder so- x=6y+15-----(2) After solving equation (1) and (2) y=270 So the correct answer is option B.

माना दो नंबर = x, y दो संख्याओं का अंतर 1365 है। x-y = 1365 ---- (1) छोटी से बड़ी संख्या को विभाजित करने पर, हमें 6 भागफल और 15 शेष मिलते हैं अतः - x= 6y + 15 ----- (2) समीकरण (1) और (2) हल करने के बाद y = 270 इसलिए सही उत्तर विकल्प B है।

Let the usual time =x min Let the usual speed=6 m/s New speed=6*7/6=7 m/s New time=(x-15) min The distance is equal so- 6*x*60 = 7*(x-15)*60 6x=7x-105 x=105 min So the correct answer is option D.

माना सामान्य समय = x मिनट माना सामान्य गति = 6 मीटर / सेकंड नई गति = 6 * 7/6 = 7 मीटर / सेकंड नया समय = (x-15) मिनट दूरी बराबर है अतः - 6 * x * 60 = 7 * (x-15) * 60 6x = 7x-105 x = 105 मिनट इसलिए सही उत्तर विकल्प D है।

H.C.F. of (4665 - 1305), (6905 - 4665) and (6905 - 1305) = H.C.F. of 3360, 2240 and 5600 N = 1120. So the Sum of digits in N = ( 1 + 1 + 2 + 0 ) = 4 So the correct answer is option A.

(4665 - 1305), (6905 - 4665) और (6905 - 1305) का H.C.F. 3360, 2240 और 5600 का H.C.F. N = 1120 तो N में अंकों का योग = (1 + 1 + 2 + 0) = 4 इसलिए सही उत्तर विकल्प A है।

1/x + 1/y +1/z = 0 yz + xz + xy/ xyz = 0 yz + xz + xy = 0-----(I) Given- x + y + z = 9-----(II) Squaring both sides (x + y + z)² = (9)² x² + y² + z² + 2xy + 2yz + 2xz = 81 x² + y² + z² + 2(xy + yz + xz) = 81 x² + y² + z² + 2(0) = 81 [from equation 1.(x+y+z=0)] x² + y² + z² = 81 ----- (III) Now- x³ + y³ + z³ - 3xyz = (x+y+z){x² + y² + z² - (xy + yz + zx)} Now put the values from equation (1) (2) and (3) x³ + y³ + z³ - 3xyz = (9)(81 - 0) x³ + y³ + z³ - 3xyz = 729 So the correct answer is option C.

1 / x + 1 / y + 1 / z = 0 yz + xz + xy / xyz = 0 yz + xz + xy = 0 ----- (I) दिया हुआ है - x + y + z = 9 ----- (II) दोनों पक्षों में वर्ग करने पर (x + y + z)² = (9)² x² + y² + z² + 2xy + 2yz + 2xz = 81 x² + y² + z² + 2(xy + yz + xz) = 81 x² + y² + z² + 2(0) = 81 [समीकरण 1 से x + y + z = 9 ] x² + y² + z² = 81 ----- (III) अब- x³ + y³ + z³ - 3xyz = (x+y+z){x² + y² + z² - (xy + yz + zx)} अब समीकरण (1) (2) और (3) से मान रखने पर- x³ + y³ + z³ - 3xyz = (9)(81 - 0) x³ + y³ + z³ - 3xyz = 729 इसलिए सही उत्तर विकल्प C है।

Let the total marks = x The minimum passing percentage for girls = 35% The minimum passing percentage for boys = 40% A boy scored 483 marks and failed by 117 marks. If the boy gets 117 more marks then it will be equal to the minimum percentage marks for the boys. So- 483 + 117 = x*40 600 = x*40/100 x = 1500 Minimum passing marks for girls are 35% of total marks, so - = 1500*35/100 = 525 So the minimum passing marks for girls are 525. So the correct answer is option B.

माना कुल अंक = x लड़कियों के लिए न्यूनतम उत्तीर्ण प्रतिशत = 35% लड़कों के लिए न्यूनतम उत्तीर्ण प्रतिशत = 40% एक लड़के ने 483 अंक हासिल किए और 117 अंक से फेल हो गया। अगर लड़के को 117 अंक और मिलते हैं तो यह लड़कों के लिए न्यूनतम प्रतिशत अंकों के बराबर होगा। इसलिए- 483 + 117 = x * 40 600 = x * 40/100 x = 1500 लड़कियों के लिए न्यूनतम उत्तीर्ण अंक कुल अंकों का 35% है, इसलिए - = 1500 * 35/100 = 525 अतः लड़कियों के लिए न्यूनतम उत्तीर्ण अंक 525 हैं। इसलिए सही उत्तर विकल्प B है।

A pipe can fill the cistern in 9 hours.

The part filled by the pipe in 1 hours = 1/9 

Due to leak the cistern fills up in 10 hours.

The part filled by pipe due to leak in the cistern = 1/10

The part emptied by the leak in 1 hours = The part filled by the pipe in 1 hours - The part filled by pipe due to leak in the cistern

= 1/9-1/10

= 10-9/90

= 1/90

So in 90 hours, the cistern will be emptied by the leak.

Hence the correct answer is option C.

एक पाइप टंकी को 9 घंटे में भर सकता है।

पाइप द्वारा 1 घंटे में भरा गया भाग = 1/9

रिसाव के कारण टंकी 10 घंटे में भर जाती है।

टंकी में रिसाव के कारण पाइप द्वारा भरा गया भाग = 1/10

1 घंटे में रिसाव द्वारा खाली किया गया भाग = 1 घंटे में पाइप द्वारा भरा गया भाग - टंकी में रिसाव के कारण पाइप द्वारा भरा गया भाग 

= 1/9-1/10

= 10-9/90

= 1/90

अत: 90 घंटे में टंकी रिसाव से खाली हो जाएगी।

अतः सही उत्तर विकल्प C है।

54 ÷ 3^2 x 6 + 3 = 54 ÷ 9 x 6 + 3 = 6 x 6 +3 = 36 + 3 = 39 So 54 3^2 x 6 + 3 = 39 So the correct answer is option B.

54 ÷ 3^2 x 6 + 3 = 54 ÷ 9 x 6 + 3 = 6 x 6 +3 = 36 + 3 = 39 अतः 54 ÷ 3^2 x 6 + 3 = 39 इसलिए सही उत्तर विकल्प B है l

Let the number=x and the quotient=y So- Number=divider*quotient+remainder x=72*y+8 When 72*y+8 is divided by 9 then- =72*y+8/9 Then the remainder will be 8. So the correct answer is option C.

माना संख्या = x और भागफल = y इसलिए- संख्या = भाजक * भागफल + शेष x= 72 * y + 8 जब 72 * y + 8 को 9 से विभाजित किया जाता है तो- = 72 * y + 8/9 अतः शेष 8 होंगा। इसलिए सही उत्तर विकल्प C है।

Length of the train = 110 m Speed of train = 60 km/hr Speed of man = 6 km/hr Relative speed = 60+6 km/hr = 66 km/hr = 66*5/18 m/s = 55/3 m/s Time =? Speed = Distance/Time 55/3 = 110/t T = 110*3/55 T = 6 sec So the train will cross the man in 6 sec. So the correct answer is option B.

ट्रेन की लंबाई = 110 मी ट्रेन की चाल = 60 किमी/घंटा आदमी की चाल = 6 किमी/घंटा सापेक्ष चाल = 60+6 किमी/घंटा = 66 किमी/घंटा = 66*5/18 मीटर/सेकंड = 55/3 मीटर/सेकेंड समय = ? चाल = दूरी/समय 55/3 = 110/T T = 110*3/55 T = 6 सेकंड अतः ट्रेन 6 सेकंड में आदमी को पार करेगी। इसलिए सही उत्तर विकल्प B है l

Total member = The money collect by all member =x According to the question- x *x =5929 x^2=5929 x=77 Total members=77 So the correct answer is option C.

कुल सदस्य = सभी सदस्य द्वारा एकत्रित धन = x प्रश्न के अनुसार- x * x = 5929 x^2 = 5929 x = 77 कुल सदस्य = 77 इसलिए सही उत्तर विकल्प C है।

Length of first train = 120 m Length of second train = 140 m Total distance covered by the both train =140+120 m = 260 m Speed of first train = 82 km/hr Speed of second train = 64 km/hr Relative speed = 82-64 = 18 km/hr = 18*5/18 m/s = 5 m/s Time = ? Speed = Distance/Time 5 = 260/t T = 52 sec So the first train will cross the second train in 52 sec. So the correct answer is option C.

पहली ट्रेन की लंबाई = 120 m दूसरी ट्रेन की लंबाई = 140 m दोनों ट्रेनों की लम्बाई या उनके द्वारा तय की गई कुल दूरी =140+120 मीटर = 260 मीटर पहली ट्रेन की चाल = 82 किमी/घंटा दूसरी ट्रेन की चाल = 64 किमी/घंटा सापेक्ष चाल = 82-64 = 18 किमी/घंटा = 18*5/18 मीटर/सेकण्ड = 5 मीटर/सेकेंड समय = ? चाल = दूरी/समय 5 = 260/T T = 52 सेकंड अतः पहली ट्रेन दूसरी ट्रेन को 52 सेकंड में पार करेगी। इसलिए सही उत्तर विकल्प C है l

(a + b) ^2 / (a^2 - b^2) =(a + b) ^2/(a+b)(a-b) =(a + b)/(a – b) So the correct answer is option C.

(a + b) ^2 / (a^2 - b^2) =(a + b) ^2/(a+b)(a-b) =(a + b)/(a – b) इसलिए सही उत्तर विकल्प C है।

(Cosec^4 A - cot^2 A) - (cot^4 A + cosec^2 A) As we know [1 + cot^2A = cosec^2A] [cosec^4A = (1 + cot^2A)^2=1 + cot^4A + 2 cot^2A] =cosec^4A – cot^4A – cot^2A – cosec^2A =1 + cot^4A + 2 cot^2A – cot^4A – cot^2A – cosec^2A = 1 + cot^2A – cosec^2A = cosec^2A - cosec^2A = 0 So the correct answer is option A.

(Cosec^4 A - cot^2 A) - (cot^4 A + cosec^2 A) हम जानते है -[1 + cot^2A = cosec^2A] [cosec^4A = (1 + cot^2A)^2=1 + cot^4A + 2 cot^2A] =cosec^4A – cot^4A – cot^2A – cosec^2A =1 + cot^4A + 2 cot^2A – cot^4A – cot^2A – cosec^2A = 1 + cot^2A – cosec^2A = cosec^2A - cosec^2A = 0 इसलिए सही उत्तर विकल्प A है।

Given - 

Speed = 330 m/sec

Time = 10 sec

Distance between fort and man = Speed*time

= 330*10

= 3300 km

= 3300/1000 m

= 3.3 m

Hence the distance between the fort and the man is 3.3 m.

So the correct answer is option C.

दिया गया है -

गति = 330 मीटर/सेकंड

समय = 10 सेकंड

किले और व्यक्ति के बीच की दूरी = गति*समय

= 330*10

= 3300 किमी

= 3300/1000 वर्ग मीटर

= 3.3 वर्ग मीटर

अत: किले और व्यक्ति के बीच की दूरी 3.3 मीटर है।

इसलिए सही उत्तर विकल्प C है।

Solution:

Total number of terms = [(last term-first term)/difference] +1

Total number of terms = [(200-101)/1]+1

= 99+1

= 100

Sum of total terms of the series = [(first term + last term /2)] x n

= [101+200/2] x 100

= [301/2] x 100

= 301 x 50

= 15050

Sum of series (101+102+103….+200) = 15050

So the correct answer is option C.

हल:

कुल पदों की संख्या = [(अंतिम पद-प्रथम पद)/सार्वांतर] +1 

कुल पदों की संख्या = [(200-101)/1]+1

= 99+1

= 100

श्रेणी की कुल पदों का योग = [(प्रथम पद + अंतिम पद /2)] x n 

= [101+200/2] x 100

= [301/2] x 100

= 301 x 50

= 15050

श्रेणी (101+102+103….+200) का योग = 15050

अतः सही उत्तर विकल्प C है l

Using remainder theorem the given expression should be equal to zero when we put x + 1 = 0 x = -1 Put x=-1 in the given equation- =x^3 + 2x^2 – 5x + k = 0 = -1^3 + 2(-1)^2 – 5 (-1) + k = 0 = k = -6 So the correct answer is option A.

शेष प्रमेय का उपयोग करते हुए दी गई अभिव्यक्ति शून्य के बराबर होनी चाहिए जब हम x + 1 = 0 रखे l x = -1 दिए गए समीकरण में x = -1 रखने पर - = x^3 + 2x^2 - 5x + k = 0 = -1^3 + 2 (-1)^2 - 5 (-1) + k = 0 = k = -6 इसलिए सही उत्तर विकल्प A है।

Let the number = 3x, 2x, 5x According to the question - (3x)^2 + (2x)^2+ (5x)^2 = 1862 9x + 4x + 25x =1862 38x = 1862 x = 49 x = 7 So the smallest number = 2x = 14 So the correct answer is option C.

माना संख्यायें = 3x, 2x, 5x प्रश्न के अनुसार - (3x)^ 2 + (2x) ^ 2 + (5x) ^ 2 = 1862 9x + 4x + 25x = 1862 38x = 1862 x = 49 x = 7। अतः सबसे छोटी संख्या = 2x = 14 इसलिए सही उत्तर विकल्प C है।

Let the principle be P. Time (t) = 16 years A sum of money double in 16 years. So - Total amount = 2P Then, Simple Interest = Total amount - Principle Simple Interest = 2P-P = P As we know - Simple Interest = P*r*t/100 P = P*r*16/100 r = 100/16 = 25/4 = 6 1/4%. Hence the Rate is 6 1/4%. So the correct answer is option D.

माना की मूलधन P है l समय (t) = 16 साल एक राशि 16 साल में दुगुनी हो जाता है। इसलिए - कुल राशि = 2P तब, साधारण ब्याज = कुल राशि - मूलधन साधारण ब्याज = 2P-P = P जैसा कि हम जानते हैं - साधारण ब्याज = P*r*t/100 P = P*r*16/100 r = 100/16 = 25/4 = 6 1/4%. अत: दर 6 1/4% है। इसलिए सही उत्तर विकल्प D है।

Let the number = x

two-fifth of the number = x*(2/5)

According to the question - x-(2/5)x = 510

= 3x/5 =510

= x =[510 * ( 5/3)]

= x = 850

So the number is 850.

Now 10% of the number -

= 10 % 0f 850

= 85

Hence the correct answer is option B.

माना संख्या = x

संख्या का 2/5 = x*(2/5)

प्रश्न के अनुसार - x-(2/5)x = 510

= 3x/5 =510

= x =[510 * ( 5/3)]

= x = 850

अतः संख्या 850 है l 

संख्या का 10% - 

= 850 का 10 %

= 85

अतः सही उत्तर विकल्प B है।

x/4 – (x – 3)/5 = 1 5x-4x+12 / 20=1 x+12=20 x=8 So the correct answer is option C

x/4 – (x – 3)/5 = 1 5x-4x+12 / 20=1 x+12=20 x=8 इसलिए सही उत्तर विकल्प C है।

Coming soon

Coming soon

√(75.24 + N ) = 8.71 75.24 + N = 8.71 x 8.71 N = 75.8641 - 75.24 N =0 .6241 Sp the correct answer is option A.

√(75.24 + N ) = 8.71 75.24 + N = 8.71 x 8.71 N = 75.8641 - 75.24 N =0 .6241 इसलिए सही उत्तर विकल्प D है।

In ꕔABC AB=3 cm BC=4 cm So by Pythagoras theorem - AC^2=AB^2+BC^2 AC^2 = (3)^2+(4)^2 AC^2=9+16 AC^2=25 AC=5 CM BD=AD=DC=Radius So BD=AC/2=5/2=2.5 cm So the correct answer is option C.

ꕔABC में AB=3 cm BC=4 cm पायथागोरस प्रमेय से - AC^2=AB^2+BC^2 AC^2 = (3)^2+(4)^2 AC^2=9+16 AC^2=25 AC=5 CM BD=AD=DC=Radius So BD=AC/2=5/2=2.5 cm इसलिए सही उत्तर विकल्प C है।

Let the numbers be 29a and 29 b. Product of numbers = Product of LCM and HCF 29a × 29b = 4147 × 29 ab = 143 ab = 11 × 13 (prime factors of 143) a=11, b=13 So the numbers are = 29a, 29b = 29*11, 29*13 The sum of the numbers = 29*11 + 29*13 =29(11+13) =29*24 =696 So the correct answer is option B.

माना संखयायें 29a और 29 b संख्याओं का गुणनखंड = LCM x HCF 29a × 29b = 4147 × 29 ab = 143 ab = 11 × 13 (143 के प्रमुख कारक) a = 11, b = 13 तो संख्याएं = 29 a, 29 b = 29 * 11, 29 * 13 संख्याओं का योग = 29*11 + 29*13 = 29 (11 + 13) = 29 * 24 = 696 इसलिए सही उत्तर विकल्प B है।

Let the salary of B = 100 rs and person A earn 50% more than that of B (100) so salary of A would be 150 rs Now B earns 50 less than person A so B's salary is less than that of A = (salay of A-salary of B/salary of A)*100 =(150-100/150)*100 =(50/150)*100 =100/3=33% So the correct ans is option B.

माना B का वेतन = 100 रुपये और व्यक्ति A ,B की तुलना में (100 ) 50% अधिक कमाता है I इसलिए A का वेतन 150 रूपये होगा I अब B व्यक्ति A से 50 रूपये कम कमाता है अतः B का वेतन A से कम है I = (A का वेतन -B का वेतन / A का वेतन ) * 100 = (150-100 / 150) * 100 = (50/150) * 100 = 100/3 = 33% इसलिए सही उत्तर विकल्प B है।

Abhinav scores 80% in physics out of 100 numbers so his physics numbers = 80 Abhinav scores 66% in chemistry out of 100 number so his chemistry numbers = 66 Let Abhinav score x numbers in maths out of 200. Total numbers = 100+100+200 = 400 He scores 80% marks in all the three subjects so - (80+66+x/400)=80/100 146+x = 320 x = 320-146 X = 174 So in math, he got 174 out of 200 so the required percentage - (174/200)*100 =87% So the correct answer is option C.

अभिनव ने 100 अंको में से फिसिक्स में 80% अंक प्राप्त किये, इसलिए उसके फिजिक्स के अंक = 80 अभिनव ने 100 में से केमिस्ट्री में 66% स्कोर किए हैं, इसलिए उसके केमिस्ट्री के अंक = 66 माना कि अभिनव ने 200 में से गणित में x अंक हासिल किए l कुल अंक = 100 + 100 + 200 = 400 वह तीनों विषयों में 80% अंक प्राप्त करता है, इसलिए - (80+66+x/400)=80/100 146+x = 320 x = 320-146 X = 174 इसलिए गणित में उन्हें 200 में से 174 मिले, अतः आवश्यक प्रतिशत - (174/200) * 100 = 87% इसलिए सही उत्तर विकल्प C है।

let sales = 100% Entry fee = 1 rs. Entry fees reduced by 25% =(1*25/100) = 0.75 sales increased by 20% = new sales =120% Now the number of visitors = (120/0.75)%= 160% increased visitors is 160% - 100% = 60% So the correct answer is option C.

माना बिक्री = 100% प्रवेश शुल्क = 1 रुपये प्रवेश शुल्क 25% कम हो गया = (1 * 25/100) = 0.75 बिक्री 20% बढ़ी = नई बिक्री = 120% अब दर्शकों की संख्या = (120 / 0.75)% = 160% दर्शकों की संख्या में वृद्धि = 160% - 100% = 60% इसलिए सही उत्तर विकल्प C है।

Pipe A can fill the tank in 60 min.

The part of the tank filled by pipe A in 1 min = 1/60

Pipe B can fill the tank in 40 min.

The part of the tank filled by pipe B in 1 min = 1/40

The part of the tank filled by both the pipes in 1 min = 1/60+1/40=2+3/120

= 5/120

= 1/24

Let the total time taken to fill the tank is x min.

Half time = x/2 min

According to the question if B is used for half the time and A and B fill it together for the other half.

The part of the tank filled by A+B in x/2 time= x/2 * 1/24 = x/48…(1)

The part of the tank filled by pipe B in x/2 time = x*2 * 1/40 = x/80…(2)

Adding (1) and (2)

x/48+x/80 = 1 work

x/48+x/80 = 1

5x+3x/240 = 1

8x/240 = 1

x/30 = 1

x = 30 min

Hence it will take 30 min to fill the empty tank.

Hence the correct answer is option D.

पाइप A टंकी को 60 मिनट में भर सकता है।

पाइप A द्वारा 1 मिनट में भरा गया टैंक का हिस्सा = 1/60

पाइप B टंकी को 40 मिनट में भर सकता है।

पाइप B द्वारा 1 मिनट में भरा गया टैंक का हिस्सा = 1/40

दोनों पाइपों द्वारा 1 मिनट में भरा गया टैंक का हिस्सा = 1/60+1/40=2+3/120

= 5/120

= 1/24

माना टंकी को भरने में लगा कुल समय x मिनट है।

आधा समय = x/2 मिनट

प्रश्न के अनुसार यदि आधे समय के लिए B का उपयोग किया जाता है और दूसरे आधे समय के लिए A और B इसे एक साथ भरते हैं।

A+B द्वारा x/2 समय में भरा गया टैंक का हिस्सा = x/2 * 1/24 = x/48…(1)

पाइप B द्वारा x/2 समय में भरा गया टैंक का हिस्सा = x*2 * 1/40 = x/80…(2)

(1) और (2) को जोड़ने पर

x/48+x/80 = 1 कार्य

x/48+x/80 = 1

5x+3x/240 = 1

8x/240 = 1

x/30 = 1

x = 30 मिनट

अतः खाली टंकी को भरने में 30 मिनट का समय लगेगा।

अतः सही उत्तर विकल्प D है।

The numbers divisible by 3 between 1 to 200=200/3=66 The numbers divisible by both 3 and 7 or 21=200/21=9 So the number between 1 to 200 which are divisible by 3 but not by 7=66-9=57 So the correct answer is option C.

1 से 200 के बीच 3 से विभाज्य संख्या= 200/3 = 66 3 और 7 दोनों या 21 से विभाज्य संख्या= 200/21 = 9 तो 1 से 200 के बीच की संख्या जो 3 से विभाज्य है, लेकिन 7 से नहीं= 66-9 = 57 इसलिए सही उत्तर विकल्प C है।

Compound Interest (C.I)= 1414.4 rs Rate (R)=8% Time (T)=2 Principle Amount (P)=? C.I. = P [(1+R/100)^T−1] = 1414.4 = P x [(1+8/100)^2-1] = 1414.4 = P x [(108/100)^2-1] = 1414.4 = P x (108 x 108/100 x 100-1) = 1414.4 = P x (11664-10000/10000) = 1414.4 = P x (1664/10000) = 1414.4 = P × 0.1664 = P = 1414.4/0.1664 = Rs.8500 Therefore amount = 8500 + 1414.14 = 9914.14 rs So the correct answer is option B.

चक्रवृद्धि ब्याज (C.I) = 1414.4 रुपये दर (R) = 8% समय (T) = 2 मूलराशि (P) =? C.I. = P [(1+R/100)^T−1] = 1414.4 = P x [(1+8/100)^2-1] = 1414.4 = P x [(108/100)^2-1] = 1414.4 = P x (108 x 108/100 x 100-1) = 1414.4 = P x (11664-10000/10000) = 1414.4 = P x (1664/10000) = 1414.4 = P × 0.1664 = P = 1414.4/0.1664 = 8500 रुपये इसलिए कुल प्राप्त राशि = 8500 + 1414.14 = 9914.14 रुपये इसलिए सही उत्तर विकल्प B है।

Let the first part =x So the second part=17500 - x Time=5 years The total interest received after 5 years is Rs 13300. So according to the question- (X × 24 ×5)/100 +{( 17500-X)×10×5}/100 =13300 (A=P x R x T /100) =120x/100+17500 *50/100 + 50x/100 =13300 =70x/100=4500 =x=6500 rs First part =6500 rs Second part=17500 - 6500=11000 rs So the ratio- =6500:11000 =13:22 So the correct answer is option D.

माना पहला भाग = x तो दूसरा भाग = 17500 - x समय = 5 वर्ष 5 वर्षों के बाद प्राप्त कुल ब्याज 13300 रुपये है। तो प्रश्न के अनुसार- (X × 24 × 5) / 100 + {(17500-X) × 10 × 5} / 100 = 13300 (A = P x R x T / 100) = 120x / 100 + 17500 * 50/100 + 50x / 100 = 13300 = 70x / 100 = 4500 = x = 6500 रू पहला भाग = 6500 रू दूसरा भाग = 17500 - 6500 = 11000 रुपये तो अनुपात- = 6500: 11000 = 13: 22 इसलिए सही उत्तर विकल्प D है।

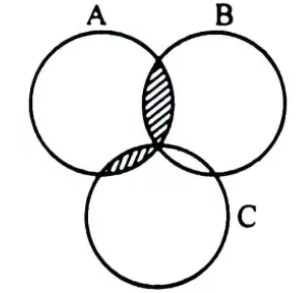
In the figure, the shaded region represents A∩(BUC).
So the correct answer is option D.

चित्र में छायांकित क्षेत्र A∩(BUC) को दर्शाता है।
इसलिए सही उत्तर विकल्प D है।

The price of shirt=1500 rs First discount =40% So the selling price=1500 x 60% Second discount=60% Then selling price=1500 x 40% x 60 % =1500 x 40/100 x 60/100 =360 rs So the correct answer is option A.

शर्ट की कीमत = 1500 रुपये पहली छूट = 40% तो बिक्री मूल्य = 1500 x 60% दूसरी छूट = 60% फिर बिक्री मूल्य = 1500 x 40% x 60% = 1500 x 40/100 x 60/100 = 360 रु इसलिए सही उत्तर विकल्प A है।

The speed of river=6 km/hr The speed of motorboat in still water= 30 km/hr Downstream speed=30+6=36 km/hr Time=24 min=24/60=0.4 hr Distance=Speed*Speed =0.4*36 =14.4 km So the correct answer is option D.

नदी की गति = 6 किमी / घंटा स्थिर पानी में मोटरबोट की गति = 30 किमी / घंटा धारा की दिशा में गति = 30 + 6 = 36 किमी / घंटा समय = 24 मिनट = 24/60 = 0.4 घंटा दूरी = चाल * गति = 0.4 * 36 = 14.4 किमी इसलिए सही उत्तर विकल्प D है।

Let two consecutive number are=x , x+1 According to the question- (x+1)^3- x^3=127 x^3+1+3x(x+1)-x^3=127 1+3x^2+3x=127 =3x^2+3x-126=0 =x^2+x+42 =x^2+(7-6)x-42 =x^2+7x-6x-42 =x=6 =x+1=7 So the numbers are=6 and 7 So the correct answer is option C.

माना दो लगातार संख्या = x, x + 1 प्रश्न के अनुसार- (x+1)^3- x^3=127 x^3+1+3x(x+1)-x^3=127 1+3x^2+3x=127 =3x^2+3x-126=0 =x^2+x+42 =x^2+(7-6)x-42 =x^2+7x-6x-42 =x=6 =x+1=7 तो संख्याएँ = 6 और 7 हैं इसलिए सही उत्तर विकल्प C है।

Let the sum be P. Rate (r) = 20% Time (t) = 3 year Difference between Compound Interest and Simple Interest is 640 Rs. Compound Interest = P[(1+r/100)^t - 1] CI = P[(1+20/100)^3 - 1] CI = P[(6/5)^3 -1] CI = P[(216/125) -1] CI = P*91/125....(1) Simple Interest = P*r*t/100 SI = P*20*3/100 SI = P*3/5...(2) According to the question - CI - SI = 372 P*91/125 - P*3/5 = 640 P(91-75)/125 = 640 P*16/125 = 640 P = 640*125/16 P = 5000 Rs Hence the sum is 5000 Rs. So the correct answer is option A.

मान लीजिए कि राशि P है। दर (r) = 20% समय (t) = 3 वर्ष चक्रवृद्धि ब्याज और साधारण ब्याज के बीच का अंतर 640 रुपये है। चक्रवृद्धि ब्याज =P[(1+r/100)^t - 1] CI = P[(1+20/100)^3 - 1] CI = P[(6/5)^3 -1] CI = P[(216/125) -1] CI = P*91/125....(1) साधारण ब्याज = P*r*t/100 SI = P*20*3/100 SI = P*3/5...(2) प्रश्न के अनुसार- CI - SI = 372 P*91/125 - P*3/5 = 640 P(91-75)/125 = 640 P*16/125 = 640 P = 640*125/16 P = 5000 रुपये अतः राशि 5000 रुपये है। इसलिए सही उत्तर विकल्प A है।

Let the smallest side=x middle side will be=x+2 Biggest side will be=x+2+2=x+4 From Paythagoras theoram- (x+4)^2=(x+2)^2+(x)^2 x=6 cm So the correct answer is option A.

सबसे छोटी भुजा = x मध्य भुजा = x + 2 सबसे बडी भुजा = x + 2 + 2 = x + 4 पयथागोरस प्रमेय से- (X + 4)^2 = (x + 2)^2 + (x)^2 x = 6 सेमी इसलिए सही उत्तर विकल्प A है।

The length of train A=220 m The length of platform=340 m The ratio of speed of trains A and B is 7 : 9, so the speed of train A will be=7x and train B=9x Time taken by train A=32 sec Time taken by train to cross the platform=(length of train A+length of platform)/speed of train A 32=(220+340)/7x 7x=560/32 x=2.5 So the speed of train B will be=9x=9*2.5=22.5 m/s The length of train B=270 m Time taken by train B to cross an electric pole=length of train B/speed of train B =270/22.5 =12 sec So the correct answer is option B.

ट्रेन A की लंबाई = 220 मीटर प्लेटफॉर्म की लंबाई = 340 मीटर ट्रेनों A और B की गति का अनुपात 7: 9 है, इसलिए ट्रेन A की गति = 7x और ट्रेन B की गति = 9x ट्रेन A द्वारा लिया गया समय= 32 सेकंड प्लेटफ़ॉर्म पार करने में ट्रेन द्वारा लिया गया समय = (ट्रेन की लंबाई A + प्लेटफ़ॉर्म की लंबाई) / ट्रेन A की गति 32 = (220 + 340) / 7x 7x = 560/32 x= 2.5 तो ट्रेन B की गति = 9x = 9 * 2.5 = 22.5 m / s ट्रेन B की लंबाई= 270 मीटर ट्रेन B द्वारा एक इलेक्ट्रिक पोल पार करने में लगने वाला समय = ट्रेन B की लंबाई / ट्रेनB की गति = 270 / 22.5 = 12 सेकंड इसलिए सही उत्तर विकल्प B है।

Time=3 year Let Amount (P)=100 rs Then Compound Money (A)=200 rs Rate=? A=P(1+R/100)^3 200=100(1+R/100)^3 2=(1+R/100)^3 ---- (1) A=P(1+R/100)^3 12800=100(1+R/100)^T 128=(1+R/100)^T 2^7=(1+R/100)^T.......(2) Put the value of equation (1) in equation (2) [(1+R/100)^3]^7=(1+R/100)^T (1+R/100)^21=(1+R/100)^T Hence, the value of T=21 years Hence, the money will become 128 times in 21 years. So the correct answer is option C.

समय = 3 वर्ष माना मूलराशि (P) = 100 रुपये तब मिश्रधन (A) = 200 rs दर (r) =? A = P (1 + r / 100) ^ 3 200 = 100 (1 + r / 100) ^ 3 2 = (1 + r / 100) ^ 3 ---- (1) A = P (1 + r/ 100) ^ 3 12800 = 100 (1 + r / 100) ^ T 128 = (1 + r / 100) ^ T 2^7 = (1 + r / 100) ^ T ....... (2) समीकरण (1) का मान समीकरण (2) में रखने पर [(1 + r / 100) ^ 3] ^ 7 = (1 + r / 100) ^ T (1 + r / 100)^21 = (1 + r / 100)^T इसलिए, T = 21 वर्ष अतः धन 21 वर्ष में 128 गुना हो जाएगा। इसलिए सही उत्तर विकल्प C है।

Three taps A, B and C can fill a tank in 20, 30 and 40 minutes respectively.

All the taps are opened simultaneously and after 5 minutes tap A was closed.

Upto 5 min the part filled by taps A, B and C = 5(1/20+1/30+1/40) = 5(6+4+3/120)

= 5(13/120)

= 65/120

After 6 minutes tab B was closed. 

Upto next 6 min the part filled by tap B and C = 6(1/30+1/40)

= 6(4+3/120)

= 6(7/120)

= 42/120

The part filled by taps A, B and C upto first 11 min = 65/120+42/120

= 107/120

Ramianing part = 1-107/120

= 13/120

Now only tap C is opened.

At the moment a leak developed which can empty the full tank in 70 minutes. 

So the part filled by tap C and leak in 1 hours = 1/40-1/70 = 7-4/280

= 3/280

Tap C and leak can fill the tank in 280/3 hours.

So 13/120 part of the tank will be fill by tap C and leak = 13/120*(280/3)

= 91/6 m

So the time taken to fill the tank completely = 11+91/6 = 66+91/6

= 26.16 min

Hence the correct answer is option B.

तीन नल A, B और C एक टंकी को क्रमशः 20, 30 और 40 मिनट में भर सकते हैं।

सभी नल एक साथ खोले जाते हैं और 5 मिनट बाद नल A को बंद कर दिया जाता है।

5 मिनट तक नल A, B और C द्वारा भरा गया भाग = 5(1/20+1/30+1/40) = 5(6+4+3/120)

= 5(13/120)

= 65/120

6 मिनट के बाद नल B को बंद कर दिया गया।

अगले 6 मिनट तक नल B और C द्वारा भरा गया भाग = 6(1/30+1/40)

= 6(4+3/120)

= 6(7/120)

= 42/120

नल A, B और C द्वारा पहले 11 मिनट तक भरा गया भाग = 65/120+42/120

= 107/120

शेष भाग = 1-107/120

= 13/120

अब केवल नल C खोला गया है।

उसी समय एक रिसाव विकसित हुआ है जो 70 मिनट में पूरे टैंक को खाली कर सकता है।

तो नल C और रिसाव द्वारा 1 घंटे में भरा गया हिस्सा = 1/40-1/70 = 7-4/280

= 3/280

नल C और रिसाव टैंक को 280/3 घंटे में भर सकता है।

तो टंकी का शेष 13/120 भाग नल C और रिसाव द्वारा भरा जाएगा = 13/120*(280/3)

= 91/6 मिनट में 

तो टंकी को पूरा भरने में लगा समय = 11+91/6 = 66+91/6

= 26.16 मि

अतः सही उत्तर विकल्प B है।

Principal (P) = 16000 Rs If the Interest is compounded quarterly. So - Rate (r) = 20% per annum= 20/4% per quarter = 5% per quarter (because there is 4 quarter in a year.) Time (t) = 9 months = 9/3 quarters = 3 quarter (because there is 3 quarter in 9 months.) Compound Interest for 1st quarter = P*r*t/100 = 16000*5*1/100 = 800 Rs Total amount after 1 quarter = 16000+800 = 16800 Rs New Principal = 16800 Rs Compund Interest for 2nd quarter = P*r*t/100 = 16800*5*1/100 = 840 Rs Total amount after 2 quarter = 16800+840 = 17640 Rs New Principal = 17640 Compund Interest for 3rd quarter = P*r*t/100 = 17640*5*1/100 = 882 Rs Hence the Total compound interest = 800+840+882 = 2522 Rs So the correct answer is option B.

मूलधन (P) = १६००० रुपये यदि ब्याज त्रैमासिक चक्रवृद्धि है। अतः - दर (r) = 20% प्रति वर्ष =20/4% प्रति तिमाही = 5% प्रति तिमाही (क्योंकि एक वर्ष में 4 तिमाही होती है।) समय (t) = 9 महीने = 9/3 तिमाही = 3 तिमाही (क्योंकि 9 महीने में 3 तिमाही होती है।) पहली तिमाही के लिए चक्रवृद्धि ब्याज = P*r*t/100 = 16000*5*1/100 = 800 रुपये 1 तिमाही के बाद कुल राशि = 16000+800 = 16800 रु नया मूलधन = 16800 रु दूसरी तिमाही के लिए चक्रवृद्धि ब्याज = P*r*t/100 = 16800*5*1/100 = 840 रुपये 2 तिमाही के बाद की कुल राशि = 16800+840 = 17640 रुपये नया मूलधन = 16840 तीसरी तिमाही के लिए चक्रवृद्धि ब्याज = P*r*t/100 = 17640*5*1/100 = 882 रुपये अत: कुल चक्रवृद्धि ब्याज = 800+840+882 = 2522 रुपये इसलिए सही उत्तर विकल्प B है।

(Cos A + Sin A) (cot A + tan A) =(Cos A + Sin A)(Cos A/Sin A+ Sin A/CosA) =(Cos A + Sin A)(Cos^2 A+Sin^2 A / Cos A . Sin A) =(Cos A + Sin A)(1/ Cos A . Sin A) =Cos A/Cos A . Sin A + Sin A/Cos A . Sin A =1/Sin A +1/Cos A =Cosec A + Sec A So the correct answer is option A.

(Cos A + Sin A) (cot A + tan A) =(Cos A + Sin A)(Cos A/Sin A+ Sin A/CosA) =(Cos A + Sin A)(Cos^2 A+Sin^2 A / Cos A . Sin A) =(Cos A + Sin A)(1/ Cos A . Sin A) =Cos A/Cos A . Sin A + Sin A/Cos A . Sin A =1/Sin A +1/Cos A =Cosec A + Sec A इसलिए सही उत्तर विकल्प A है।

Given - Total Population = 728400 Migrants are 35% of Total population = 35 % of 728400 = 254940 local population = Total Population - Migrants = (728400 - 254940) = 473460. Rural migrants = 20% of 254940 = 50988 Urban migrants = (254940 - 50988) = 203952 So according to the question - Female population = 48% of 473460 + 30% of 50988 + 40% of 203952 2,27,260.8 + 15,296.4 + 81,580.8 = 324138 So the correct answer is option A.

दिया हुआ - कुल जनसंख्या = 728400 प्रवासियों कुल जनसंख्या का 35% है = 728400 का 35% = 254940 ह स्थानीय जनसंख्या = कुल जनसंख्या - प्रवासी = (728400 - 254940) = 473460 ग्रामीण प्रवासी = 254940 का 20% = 50988 शहरी प्रवासी = (254940 - 50988) = 203952 तो प्रश्न के अनुसार - महिला जनसंख्या = 473460 का 48% + 50988 का 30% + 203952 का 40% 2,27,260.8 + 15,296.4 + 81,580.8 = 324138 इसलिए सही उत्तर विकल्प A है।

Let faster pipe can filled the reservoir in x hours. So in 1 hour the faster pipe can fill the part=1/x So the slower pipe will fill the reservoir in (x+20) hours. So in 1 hour the slower pipe can fill the part=1/(x+20) If two pipes function simultaneously, the reservoir will be filled in 24 hrs so- 1/x+1/(x+20)=1/24 x+20+x/(x(x+20))=1/24 (2x+20)24=x^2+20x 48x+480=x^2+20x x^2-28x-480=0 x^2-40x+12x-480=0 x(x-40)+12(x-40)=0 x=40 hours So the correct answer is option C.

माना तेज़ पाइप से जलाशय x घंटे भर सकता हैं। तब 1 घंटे में तेज पाइप भाग भर सकता है= 1 / x तो धीमा पाइप जलाशय को (x + 20) घंटों में भर देगा। तो 1 घंटे में धीमा पाइप भाग को भर सकता है = 1 / (x + 20) यदि दो पाइप एक साथ काम करते हैं, तो जलाशय 24 घंटे में भर जाएगा। 1 / x + 1 / (x+ 20) = 1/24 x + 20 + x / (x(x + 20)) = 1/24 (2x + 20) 24 = x ^ 2 + 20x 48x + 480 = x ^ 2 + 20x x^2-28x-480 = 0 x^2-40x + 12x-480 = 0 x (x- 40)+ 12 (x -40) = 0 x = 40 घंटे इसलिए सही उत्तर विकल्प C है।

To solve this question, we can divide 28 May 2006 into small parts.

To 28 May 2006, we can write (2000 + 5 + 1 January 2006 + 28 May 2006).

2000 = 1600 + 400 = 0 odd days + 0 odd days = 0 odd days 

Now we will find the number of odd days From 2000 to 2005. 

Odd days in 5 years = 4 ordinary years + 1 leap year (2004 is leap year between 2000 and 2005)

Odd days in an ordinary year = 1

Odd days in leap year = 2

Odd days in 5 years = 4*1 + 1*2 = 4+2 = 6 odd days

Total number of days from 1st Jan 2006 to 28th May 2006

January+February+March+April+28 days (May days)

31 +28+31+30+28 = 148 days

Odd days in 148 days = 148/7 = 21 + 1 remainder

Hence number of odd days in 148 days = 1

Total odd days = 0 + 6+1 = 7 

odd days = 0

Hence 28th May 2006 was Sunday.

So the correct answer is option D.

इस प्रश्न को हल करने के लिए हम 28 मई 2006 को छोटे छोटे भागों में विभाजित कर सकते है l 

28 मई 2006 को हम (2000 + 5 + 1 जनवरी 2006 + 28 मई 2006) लिख सकते है l 

2000 = 1600+400 = 0 विषम दिन + 0 विषम दिन = 0 विषम दिन

अब हम 2000 से 2005 तक विषम दिनों की संख्या ज्ञात करेंगे। 

5 वर्ष में विषम दिन = 4 साधारण वर्ष + 1 लीप वर्ष (2000 से 2005 के बीच 2004 लीप वर्ष है)

साधारण वर्ष में विषम दिन = 1 

लीप वर्ष में विषम दिन = 2 

5 वर्ष में विषम दिन = 4*1 + 1*2 = 4+2 = 6 विषम दिन 

1 जनवरी 2006 से 28 मई 2006 तक कुल दिनों की संख्या 

जनवरी+फरवरी +मार्च+अप्रैल+28 (मई के दिन)

31 +28+31+30+28 = 148 दिन 

148 दिनों में विषम दिन = 148/7 = 21 + 1 शेषफल 

अतः 148 दिनों में विषम दिनों की संख्या = 1 

कुल विषम दिन = 0 + 6+1 = 7 

विषम दिन = 0 

अतः 28 मई 2006 को रविवार था l 

इसलिए सही उत्तर विकल्प D है l

F-4=B G-4=C H-4=D I-4=E O-4=K P-4=L Q-4=M R-4 =N So the correct answer is option B.

F-4=B G-4=C H-4=D I-4=E O-4=K P-4=L Q-4=M R-4 =N इसलिए सही उत्तर विकल्प B है।

ACOUSTIC=A+C+O+U+S+T+I+C=91 RENOUNCE=R+E+N+O+U+N+C+E=95 So the correct answer is option A.

ACOUSTIC=A+C+O+U+S+T+I+C=91 RENOUNCE=R+E+N+O+U+N+C+E=95 इसलिए सही उत्तर विकल्प A है।

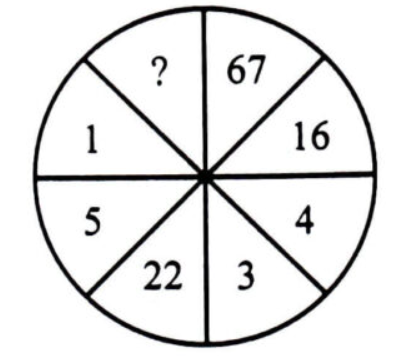
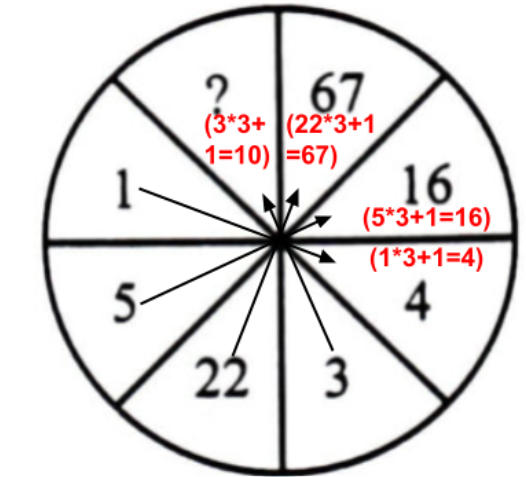
The missing number is 10.
So the correct answer is option C.
You can see its solution in the picture below.

लुप्त संख्या 10 है। 
इसलिए सही उत्तर विकल्प C है। 
इसका समाधान आप नीचे दिए गए चित्र में देख सकते है। 

Click here to Take a free reasoning mock test.

Coming soon

Coming soon

Bow is to Violin as Plectrum is to Sitar. So the correct answer is option C.

बो वायलिन से उसी प्रकार सम्बंधित है जैसे पल्ट्रम सितार से I इसलिए सही उत्तर विकल्प C है।

Relation between EGIK : 691215 E(5)+1 = 6 G(7)+2 = 7 I(9)+3 = 12 K(11)+4 = 15 Similarly - C(3)+1 = 4 E(5)+2 = 7 H(8)+3 = 11 P(16)+4 = 20 Hence the related letters are CEHP. So the correct answer is option B.

EGIK: 691215 के बीच संबंध E(5)+1 = 6 G(7)+2 = 7 I(9)+3 = 12 K(11)+4 = 15 इसी प्रकार - C(3)+1 = 4 E(5)+2 = 7 H(8)+3 = 11 P(16)+4 = 20 अतः संबंधित अक्षर CEHP हैं। इसलिए सही उत्तर विकल्प B है।

Brick is different from other, because Temple,Palace,and House all are build by Bricks. So the correct answer is option B.

ईंट दूसरे से अलग है, क्योंकि मंदिर, महल और घर सभी ईंटों द्वारा निर्मित होते हैं। इसलिए सही उत्तर विकल्प B है।

The figure given in Option D is embedded in the question figure.

So the correct answer is option D.

विकल्प D में दी गयी आकृति प्रश्न आकृति में निहित है।

इसलिए सही उत्तर विकल्प D है।

7 = (2^3 - 1), 26 = (3^3 - 1), 63 = (4^3 - 1), 124 = (5^3 - 1), 215 = (6^3 - 1), 342 = (7^3 - 1), 8^3-1 = 511 Hence, the next number is 511. So the correct answer is option D.

7 = (2^3 - 1), 26 = (3^3 - 1), 63 = (4^3 - 1), 124 = (5^3 - 1), 215 = (6^3 - 1), 342 = (7^3 - 1), 8^3-1 = 511 अतः, अगली संख्या 511 है। इसलिए सही उत्तर विकल्प D है।

7, 10, 8, 11, 9, 12, ... There are two series first is =7, 8, 9,10 Second series is =10,11,12,13 So the correct answer is option B.

7, 10, 8, 11, 9, 12, ... यहाँ दो श्रृंखलाएँ हैं पहली श्रंखला -7,8,9,10 दूसरी श्रृंखला है -10,11,12,13 इसलिए सही उत्तर विकल्प B है।

2, 3, 10, 38, 172

2 × 1 + 1² = 3,

3 × 2 + 2² =10,

10 × 3 + 3² = 39,

39 × 4 + 4² = 172

Hence 38 is the wrong number and in place of 38, it should be 39. So the correct answer is option A.

2, 3, 10, 38, 172

2 × 1 + 1² = 3,

3 × 2 + 2² =10,

10 × 3 + 3² = 39,

39 × 4 + 4² = 172

अत: 38 गलत संख्या है और 38 के स्थान पर 39 होनी चाहिए। इसलिए सही उत्तर विकल्प A है।

In the series, each letter is given its alphabetical series number and one letter is skipped in between.

C-3, 

E-5, 

G-7, 

I-9,

K-11

M-13

So the missing letters and number are K-11, M-13.

Hence the correct answer is option A.

श्रृंखला में, प्रत्येक अक्षर को उसकी वर्णमाला श्रृंखला संख्या दी गई है और बीच में एक अक्षर को छोड़ दिया गया है।

C-3, 

E-5, 

G-7, 

I-9,

K-11

M-13

लुप्त अक्षर और संख्या K-11, M-13 हैं।

अतः सही उत्तर विकल्प A है।

xyzk/xyzk/xyzk/xyzk/x So the correct answer is option A.

xyzk/xyzk/xyzk/xyzk/x इसलिए सही उत्तर विकल्प A है।

8 x 1 - 2 = 6 6 x 2 - 3 = 9 9 x 3 - 4 = 23 23 x 4 - 5 = 87 87 x 5 - 6 = 429 So the correct answer is option D.

8 x 1 - 2 = 6 6 x 2 - 3 = 9 9 x 3 - 4 = 23 23 x 4 - 5 = 87 87 x 5 - 6 = 429 इसलिए सही उत्तर विकल्प D है।

Just as a voyage causes Sea sickness, similarly, climbing at a height causes Giddiness.

So the correct answer is option C.

जिस प्रकार जहाजी यात्रा करने से जहाजी मतली होती है उसी प्रकार ऊंचाई पर चढ़ने से चक्कर (सिर में) आने लगता है l 

इसलिए सही उत्तर विकल्प C है l 

There are 45 trees in a row. The rank of lemon tree from the right end= 20th So the rank of lemon tree from the left end= 45 - 20 +1=26th So the correct answer is option A.

एक पंक्ति में 45 पेड़ हैं। दायें ओर से नींबू के पेड़ की रैंक=20वीं तो बाएं पेड़ से नींबू का पेड़ की रैंक= 45 - 20 +1=26वीं इसलिए सही उत्तर विकल्प A है।

The woman seen in the picture is the mother of the woman speaking. And the son of the woman with the picture is the brother of the speaking woman. The speaking woman's brother is Pramod's maternal uncle. Hence the woman speaking is the wife of Pramod's father. So the correct answer is option D.

तस्वीर में दिख रही महिला बोलने वाली महिला की माँ है। और तस्वीर वाली महिला का बेटा बोलने वाली महिला का भाई है बोलने वाली महिला का भाई प्रमोद का मामा है। अतः बोलने वाली महिला प्रमोद के पिता की पत्नी है। इसलिए सही उत्तर विकल्प D है।

Option C will replace the question mark (?).

So the correct answer is option C.

विकल्प C प्रश्नवाचक चिन्ह (?) का स्थान लेगा।

इसलिए सही उत्तर विकल्प C है।

Jailor is the keeper of Prison and Curator is the keeper of a museum or other collection. So the correct answer is option B.

जेलर जेल का रक्षक है और क्यूरेटर एक संग्रहालय या अन्य संग्रह का रक्षक है। इसलिए सही उत्तर विकल्प B है।

There are three modes of losing Indian Citizenship. Renunciation,Termination and Deprivation. So the correct answer is option D.

भारतीय नागरिकता को खोने के तीन तरीके है - स्वयं परित्याग करने से , अन्य देश की नागरिकता ग्रहण करने से और संघ द्वारा नागरिकता अपहरण से l इसलिए सही उत्तर विकल्प D है।

Godavari river is known as Dakshina Ganga. The Godavari is the largest river in peninsular India. So the correct answer is option B.

गोदावरी नदी को दक्षिणा गंगा के नाम से जाना जाता है। गोदावरी प्रायद्वीपीय भारत की सबसे बड़ी नदी है । इसलिए सही उत्तर विकल्प B है।

As per Asoka’s inscriptions of Nigliva and Rumindei, Lumbini was declared tax free and proclaimed only 1/8th part as taxable. So the correct answer is option B.

अशोक के निग्लिवा और रुमिन्देई के शिलालेखों के अनुसार, लुम्बिनी को कर मुक्त घोषित किया गया और केवल 1/8 वें भाग को कर योग्य घोषित किया गया। इसलिए सही उत्तर विकल्प B है।

A "closed economy" is an economy in which Neither exports nor imports take place. A closed economy is one that has no trading activity with outside economies. The closed economy is therefore entirely self-sufficient. An open economy is an economy in which there are economic activities between the domestic community and outside. So the correct answer is option D.

एक "बंद अर्थव्यवस्था" एक ऐसी अर्थव्यवस्था है जिसमें न तो निर्यात होता है और न ही आयात होता है। एक बंद अर्थव्यवस्था वह है जिसमें बाहरी अर्थव्यवस्थाओं के साथ कोई व्यापारिक गतिविधि नहीं है। इसलिए बंद अर्थव्यवस्था पूरी तरह से आत्मनिर्भर है। एक खुली अर्थव्यवस्था एक ऐसी अर्थव्यवस्था है जिसमें घरेलू समुदाय और बाहर के बीच आर्थिक गतिविधियां होती हैं। इसलिए सही उत्तर विकल्प D है।

Sound waves in air are longitudinal. So the correct answer is option C.

हवा में ध्वनि तरंगें अनुदैर्ध्य होती हैं। इसलिए सही उत्तर विकल्प C है।

The basic regulatory authority for mutual funds and stock markets lies with SEBI (Securities and Exchange Board of India). So the correct answer is option B.

म्यूचुअल फंड और शेयर बाजार के लिए मूल नियामक प्राधिकरण सेबी (भारतीय प्रतिभूति और विनिमय बोर्ड) के अंतर्गत है। इसलिए सही उत्तर विकल्प B है।

Plants that grow in saline water are called Halophytes. So the correct answer is option A.

खारे पानी में उगने वाले पौधों को हेलोफाइट्स कहा जाता है। इसलिए सही उत्तर विकल्प A है।

The aim of the First Five Year Plan was to correct the disequilibrium in the economy. The first Indian Prime Minister, Jawaharlal Nehru presented the first five-year plan to the Parliament of India and wanted immediate attention. The first five-year plan was launched in 1951, which focused mainly on the development of the primary sector. The first five-year plan was based on the Harrod – Domar model with some modifications. So the correct answer is option A.

प्रथम पंचवर्षीय योजना का उद्देश्य अर्थव्यवस्था में असमानता को दूर करना था। प्रथम भारतीय प्रधान मंत्री, जवाहरलाल नेहरू ने भारत की संसद को पहली पंचवर्षीय योजना प्रस्तुत की और इस पर तत्काल ध्यान चाहते थे । प्रथम पंचवर्षीय योजना 1951 में शुरू की गई थी, जिसमें मुख्य रूप से प्राथमिक क्षेत्र के विकास पर ध्यान केंद्रित किया गया था। पहली पंचवर्षीय योजना कुछ संशोधनों के साथ हैरोड-डोमर मॉडल पर आधारित थी। इसलिए सही उत्तर विकल्प A है।

Everything we eat is made up of Molecules. So the correct answer is option A.

हम जो कुछ भी खाते हैं वह अणु से बना होता है। इसलिए सही उत्तर विकल्प A है।

Moon is a good example of Non-luminous objects. Non- luminous- bodies that don't have light of their own. example - Pencil , Paper , Rock, Moon Moon is a non luminous body as it doesn't emits light of itself. we can see the moon in the sky because it reflects the light of sun Luminous- bodies that emit light of their own. example- Sun, Star So the correct answer is option C.

चंद्रमा गैर-चमकदार वस्तुओं का एक अच्छा उदाहरण है। गैर-चमकदार वस्तुए जिनके पास स्वयं का प्रकाश नहीं है। उदाहरण - पेंसिल, पेपर, रॉक, मून चंद्रमा एक गैर चमकदार वस्तु है क्योंकि यह स्वयं प्रकाश का उत्सर्जन नहीं करता है। हम आकाश में चंद्रमा को देख सकते हैं क्योंकि यह सूर्य के प्रकाश को परावर्तित करता है l चमकदार वस्तु - वस्तुए जो अपने स्वयं के प्रकाश का उत्सर्जन करते हैं। उदाहरण- सूर्य, तारा इसलिए सही उत्तर विकल्प C है।

Gangavaram Port of Andhra Pradesh is the deepest port in India. The Gangavaram Port has opened in 2009 July by the former chief minister of Andhra Pradesh, Shri Y S Rajasekhara Reddy. Before it Vishakhapatnam was the deepest port. So the correct answer is option D.

आंध्र प्रदेश का गंगावरम बंदरगाह भारत का सबसे गहरा बंदरगाह है। गंगावरम बंदरगाह 2009 में आंध्र प्रदेश के पूर्व मुख्यमंत्री श्री वाई एस राजशेखर रेड्डी द्वारा खोला गया है। इससे पहले विशाखापट्टनम सबसे गहरा बंदरगाह था। इसलिए सही उत्तर विकल्प D है।

Naturalization , Descent , Acquiring Foreign Territory all are the modes of acquiring Indian Citizenship. So the correct answer is option D.

देशीकरण , वंश, विदेशी क्षेत्र का अधिग्रहण करना सभी भारतीय नागरिकता प्राप्त करने के तरीके हैं। इसलिए सही उत्तर विकल्प D है।

Myopia is associated with eyes. Myopia, also called myopia, is an eye defect in which patients are not able to see objects clearly over long distances. To correct this defect, an ambulatory lens is used. So the correct answer is option A.

मायोपिया आँखों से जुड़ा हुआ है। मायोपिया, जिसे निकट दृष्टिदोष भी कहा जाता है, एक आंख का दोष है जिसमें रोगी लंबी दूरी पर वस्तुओं को स्पष्ट रूप से नहीं देख पाते हैं। इस दोष को ठीक करने के लिए, एक उभयावतल लेंस का उपयोग किया जाता है। इसलिए सही उत्तर विकल्प A है।

To open an existing workbook, click the open button on the Standard toolbar. So the correct answer is option B.

किसी मौजूदा कार्यपुस्तिका को खोलने के लिए, स्टैण्डर्ड टूलबार पर ओपन बटन पर क्लिक करें। इसलिए सही उत्तर विकल्प B है।

The red data book contains data for all endangered species. The Red Data Book has been established by the IUCN to document rare and endangered species of plants, animals, fungi, and some local species that exist within a state or country. So the correct answer is option C.

लाल डेटा बुक में सभी लुप्तप्राय प्रजातियों के डेटा शामिल हैं। रेड डेटा बुक IUCN द्वारा पौधों, जानवरों, कवक और कुछ स्थानीय प्रजातियों की दुर्लभ और लुप्तप्राय प्रजातियों के दस्तावेज के लिए स्थापित किया गया है जो एक राज्य या देश के भीतर मौजूद हैं। इसलिए सही उत्तर विकल्प C है।

A cash crop or profit crop is an agricultural crop that is sold for profit. In less developed countries, cash crops are usually crops that attract demand in more developed countries and therefore have some export value. Some examples of cash crops are - coffee, groundnut, cocoa, tea, sugarcane, cotton, tobacco, cotton, jute, spices, and oilseeds, etc. Cotton is one of the most important cash crops in India. So the correct answer is option A.

नकदी फसल या लाभ की फसल एक कृषि फसल है जिसे लाभ के लिए बेचा जाता है। कम विकसित देशों में, नकदी फसलें आमतौर पर ऐसी फसलें होती हैं, जो अधिक विकसित देशों में मांग को आकर्षित करती हैं, और इसलिए इनका कुछ निर्यात मूल्य होता है। नकदी फसलों के कुछ उदाहरण हैं -कॉफी, मूंगफली, कोको, चाय, गन्ना, कपास, तंबाकू, कपास, जूट, मसाले और तिलहन आदि l कपास भारत की सबसे महत्वपूर्ण नकदी फसल में से एक है। इसलिए सही उत्तर विकल्प A है।

Black revolution is related to the Crude oil production. Blue Revolution - Related with Fish Production Golden Revolution - Related with Overall Horticulture, Honey, Fruit Production Brown Revolution - Related with Leather, Cocoa Pink Revolution - Related with Onions, Prawn Round Revolution - Related with Potato Production Grey Revolution - Related with Fertilizers White Revolution - Related with Dairy, Milk Production Silver Revolution - Related with Egg Production Yellow Revolution - Related with Oil Seed Production So the correct answer is option C.

काली क्रांति कच्चे तेल उत्पादन से संबंधित है। नीली क्रांति - मछली उत्पादन से संबंधित स्वर्ण क्रांति - समग्र बागवानी, शहद, फल उत्पादन से संबंधित भूरी क्रांति - चमड़ा, कोको से संबंधित गुलाबी क्रांति - प्याज से संबंधित, झींगा गोल क्रांति - आलू उत्पादन से संबंधित ग्रे क्रांति - उर्वरकों के साथ संबंधित श्वेत क्रांति - डेयरी, दुग्ध उत्पादन से संबंधित रजत क्रांति - अंडा उत्पादन से संबंधित पीली क्रांति - तेल बीज उत्पादन से संबंधित इसलिए सही उत्तर विकल्प C है।

Rakesh Mohan Committee was for formulating the framework of restructuring railways. So the correct answer is option C.

राकेश मोहन समिति रेलवे के पुनर्गठन की रूपरेखा तैयार करने के लिए बनाई गयी थी। इसलिए सही उत्तर विकल्प C है।

Boat race is part of Onam festival. Onam is a "harvest festival" generally celebrated in the state of "Kerala" of India . So the correct answer is option B.

नौका दौड़ ओणम त्योहार का हिस्सा है। ओणम एक "फसल उत्सव" है जो आम तौर पर भारत के "केरल" राज्य में मनाया जाता है। इसलिए सही उत्तर विकल्प B है।

Himalayan mountain range falls under Fold Mountain. The Himalayas are fold mountains that were formed when the Eurasian plate and Indian Plate collided. Initially, there was an ocean, called Tethys sea, where the Himalayas is today. So the correct answer is option D.

हिमालय पर्वत श्रृंखला वलित पर्वत के अंतर्गत आती है। हिमालय वलित पर्वत हैं जो यूरेशियन प्लेट और इंडियन प्लेट के टकराने से बना था । जहां आज हिमालय है, प्रारंभ में वहाँ एक महासागर था, जिसे टेथिस समुद्र कहा जाता था । इसलिए सही उत्तर विकल्प D है।

Vitamin C is not a fat-soluble vitamin it is a water-soluble vitamin. The fat-soluble vitamins are vitamin - A, D, E, and K. So the correct answer is option C.

विटामिन सी वसा में घुलनशील विटामिन नहीं है, यह पानी में घुलनशील विटामिन है। विटामिन A,D, E और K वसा में घुलनशील विटामिन हैं। इसलिए सही उत्तर विकल्प C है।

The SI unit of electric current is Ampere. So the correct answer is option C.

विद्युत धारा की SI इकाई एम्पीयर है। इसलिए सही उत्तर विकल्प C है।

The speed of light will be minimum while passing through Glass. The speed of light will be maximum while passing through Vaccum. So the correct answer is option A.

कांच से गुजरते समय प्रकाश की गति न्यूनतम होगी। निर्वात से गुजरते समय प्रकाश की गति अधिकतम होगी। इसलिए सही उत्तर विकल्प A है।

Product of Force and Velocity is called Power. So the correct answer is option D.

बल और वेग के उत्पाद को शक्ति कहा जाता है। इसलिए सही उत्तर विकल्प D है।

V cholera was first isolated as a cause of cholera in 1854 by Filippo Pakini, but his discovery was not widely known as Robert Koch (who also discovered tuberculosis). So the correct answer is option A.

वी हैजा को पहली बार 1854 में फिलिपो पाकिनी द्वारा हैजे के कारण के रूप में अलग किया गया था, लेकिन उनकी खोज को रॉबर्ट कोच (जिन्होंने तपेदिक का कारण भी खोजा) जैसे व्यापक रूप से नहीं जाना गया था l इसलिए सही उत्तर विकल्प A है।

If a sound travels from air to water, the quantity that remain unchanged is Frequency but Wavelength,Velocity and Amplitude definitely changes. So the correct answer is option A.

यदि कोई ध्वनि हवा से पानी में प्रवेश करती है, तो जो मात्रा अपरिवर्तित रहती है, वह आवृत्ति होती है, लेकिन तरंगदैर्ध्य, वेग और आयाम निश्चित रूप से परिवर्तित होते हैं। इसलिए सही उत्तर विकल्प A है।

Synapse is not a part of a neuron. So the correct answer is option D.

सिनैप्स न्यूरॉन का हिस्सा नहीं है। इसलिए सही उत्तर विकल्प D है।

"Image that is created in plane mirror is virtual". statement is Right. So the correct answer is option A.

"समतल दर्पण में बनाई गई छवि आभासी होती है"। कथन सही है। इसलिए सही उत्तर विकल्प A है।

Liver is the largest gland in human body. The second largest gland in human body is pancreas. Pituitary gland is the smallest gland of human body. So the correct answer is option B.

लिवर मानव शरीर की सबसे बड़ी ग्रंथि है। मानव शरीर में दूसरी सबसे बड़ी ग्रंथि अग्न्याशय है। पिट्यूटरी ग्रंथि मानव शरीर की सबसे छोटी ग्रंथि है। इसलिए सही उत्तर विकल्प B है।

Vitamin B12 is also known as cobalamin. So the correct answer is option A.

विटामिन बी-12 को कोबालिन के रूप में भी जाना जाता है। इसलिए सही उत्तर विकल्प A है l

Appearance of Plasma is Yellow in colour. Plasma makes up the biggest part (about 55%) of your blood and contains water(90%), salts, enzymes, antibodies and other proteins. So the correct answer is option B.

प्लाज़्मा का रंग पीला होता है। प्लाज्मा आपके रक्त का सबसे बड़ा हिस्सा (लगभग 55%) बनाता है और इसमें पानी (90%), लवण, एंजाइम, एंटीबॉडी और अन्य प्रोटीन होते हैं। इसलिए सही उत्तर विकल्प B है।

The virus causes diseases such as polio (poliovirus) and chicken pox (varicella - zoster virus). The virus was discovered in the tobacco plant (tobacco mosaic virus) by Dmitry Ivanowski. So the correct answer is option C.

वायरस , पोलियो (पोलियोवायरस) और चिकन पॉक्स (वैरिकाला - जोस्टर वायरस) जैसी बीमारियों का कारण बनता है। दिमित्री इवानोव्स्की ने तंबाकू के पौधे (तम्बाकू मोज़ेक वायरस) में वायरस की खोज की थी । इसलिए सही उत्तर विकल्प C है।

To enter the blood vessels, large molecules are digested. Digestion is the breakdown of large insoluble food molecules into small water-soluble food molecules so that they can be absorbed into the blood plasma of water. So the correct answer is option C.

रक्त वाहिकाओं में प्रवेश करने के लिए, बड़े अणुओं का पाचन होता है। पाचन , बड़े अघुलनशील खाद्य अणुओं के छोटे पानी में घुलनशील खाद्य अणुओं का टूटना है, ताकि उन्हें पानी के रक्त प्लाज्मा में अवशोषित किया जा सके। इसलिए सही उत्तर विकल्प C है।

Sound of frequency below 20 Hz is called Infrasonic. Infrasound is too low for humans to hear. Sound of frequencies above 20,000 hertz is called Ultrasonic. sound of frequency in between 20 Hz to 20 kHz is called as audio sound. So the correct answer is option A.

20 हर्ट्ज से कम की आवृत्ति वाली ध्वनि को इन्फ्रासोनिक कहा जाता है। यह मनुष्यों को सुनने के लिए बहुत कम है। 20,000 हर्ट्ज से अधिक आवृत्तियों की ध्वनि को अल्ट्रासोनिक कहा जाता है। 20 हर्ट्ज से 20 kHz के बीच आवृत्ति की ध्वनि को ऑडियो ध्वनि कहा जाता है। इसलिए सही उत्तर विकल्प A है।

The process of gaining electrons is known as reduction. The process in which a substance loses an electron in a chemical reaction is called oxidation. So the correct answer is option B.

इलेक्ट्रॉनों को प्राप्त करने की प्रक्रिया को अपचयन के रूप में जाना जाता है l वह प्रक्रिया जिसमें कोई पदार्थ रासायनिक प्रतिक्रिया में एक इलेक्ट्रॉन खो देता है, ऑक्सीकरण कहलाती है। इसलिए सही उत्तर विकल्प B है।