The Indian Statistical Service (ISS) is a civil service under Group A of the Central Civil Services of the executive branch of the Government of India. Indian Statistical Service (ISS) is the All India Exam that is conducted annually by the UPSC. The Indian Statistical Service (ISS) examination 2020 will be conducted between 16 to 18 October.
Click here to Download Notification for UPSC ISS Exam 2020
Total: 47 Post
Click here to Download Admit Card for UPSC ISS Exam 2020
(I) Nationality
A candidate must be either:—
(a) a citizen of India; or
(b) a subject of Nepal; or
(c) a subject of Bhutan; or
(d) a Tibetan refugee who came over to India, before the 1st January 1962, with the intention of permanently settling in India; or
(e) a person of Indian origin who has migrated from Pakistan, Burma, Sri Lanka, East African countries of Kenya, Uganda, the United Republic of Tanzania, Zambia, Malawi, Zaire, and Ethiopia or Vietnam with the intention of permanently settling in India :
Provided that a candidate belonging to categories (b), (c), (d) & (e) above shall be a person in whose favor a certificate of eligibility has been issued by the Government of India.
A candidate in whose case a certificate of eligibility is necessary may be admitted to the examination but the offer of appointment may be given only after the necessary eligibility certificate has been issued to him/her by the Government of India.
(II) Education Qualifications :
The candidates must have obtained a Bachelor's Degree with Statistics/Mathematical Statistics/Applied Statistics as one of the subjects or else the candidates should hold a Master's degree in Statistics/Mathematical Statistics/Applied Statistics from a recognized university or a foreign university approved by the Central Government of India from time to time.
(III)Age limit:
|
Category |
Age relaxation |
|
Scheduled Caste(SC) |
5 years |
|
Scheduled Tribe (ST) |
5 years |
|
A person who has ordinarily been domiciled in the State of Jammu & Kashmir during the period from January 1, 1980, to December 31, 1989 |
5 years |
|
Defense Services Personnel disabled in operations during hostilities with any foreign country or in a disturbed area and released as a consequence thereof |
Up to 3 years |
|
ex-servicemen including Commissioned Officers and ECOs/SSCOs who have rendered at least five years Military Service as of August 1, 2020 |
Up to 5 years |
|
A person with physical disabilities |
Up to 10 years |
Note:
(IV) Physical Standards: Candidates must be physically fit according to physical standard for admission to Indian Economic Service Examination, 2020 as per Regulations given in Appendix III of the rules for the Indian Economic Service Examination, 2020 published in Gazette of India dated 11th August 2020.
The selection process of UPSC IES comprises two stages. The two stages are -
Stage I: Written Exam of 1000 marks
Stage II: Viva-voce or Interview of 200 marks
|
Subject |
Marks |
Time Duration |
|
General English |
100 |
3 hours |
|
General Studies |
100 |
3 hours |
|
Statistics I (Objective) |
200 |
2 hours |
|
Statistics II (Objective) |
200 |
2 hours |
|
Statistics III (Descriptive) |
200 |
3 hours |
|
Statistics IV (Descriptive) |
200 |
3 hours |
Note-1: Statistics I & II will be of Objective Type Questions (80 questions with maximum marks of 200 in each paper) to be attempted in 120 minutes.
Note-2: Statistics III and IV will be of Descriptive Type having Short Answer/ Small Problems Questions (50%) and Long Answer and Comprehension problem questions (50%). At least one Short Answer and One Long Answer Question from each section are compulsory. In Statistics-IV, an equal number of questions i.e. 50% weightage from all the sub-sections below, and candidates have to choose any two subsections and answer.
Note-3: The papers on General English and General Studies will be of subjective type.
Note-4: The details of the standard and syllabi for the examination are given in Section-II below.
2. The question papers in all subjects will be of Conventional (essay) type except in Statistics Paper I and Statistics Paper-II which are Objective Type Papers.
The candidate will be interviewed by a Board of competent and unbiased observers who will have before them a record of his/her career. The object of the interview is to assess his/her suitability for the service for which he/she has competed. The interview is intended to supplement the written examination for testing the general and specialized knowledge and abilities of the candidate. The candidate will be expected to have taken an intelligent interest not only in his/her subjects of academic study but also in events which are happening around him/her both within and outside his/her own State or Country as well as in modern currents of thought and in new discoveries which should arouse the curiosity of well-educated youth.
The technique of the interview is not that of a strict cross-examination, but of a natural, though directed and purposive conversation intended to reveal the candidate's mental qualities and his/her grasp of problems. The Board will pay special attention to assess the intellectual curiosity, critical powers of assimilation, the balance of judgment and alertness of mind, the ability for social cohesion, the integrity of character initiative, and capacity for leadership.
The standard of papers in General English and General Studies will be such as may be expected of a graduate of an Indian University.
The standard of papers in the other subjects will be that of the Master’s degree examination of an Indian University in the relevant disciplines. The candidates will be expected to illustrate the theory by facts, and to analyze problems with the help of theory. They will be expected to be particularly conversant with Indian problems in the field(s) of Statistics.
GENERAL ENGLISH
Candidates will be required to write an essay in English. Other questions will be designed to test their understanding of English and workman-like use of words. Passages will usually be set for summary or precis.
GENERAL STUDIES
General knowledge including knowledge of current events and of such matters of everyday observation and experience in their scientific aspects as may be expected of an educated person who has not made a special study of any scientific subject. The paper will also include questions on Indian Polity including the political system and the Constitution of India, History of India, and Geography of nature which a candidate should be able to answer without special study.
STATISTICS-I (OBJECTIVE TYPE)
(i) Probability
Classical and axiomatic definitions of Probability and consequences. Law of total probability, Conditional probability, Bayes' theorem, and applications. Discrete and continuous random variables. Distribution functions and their properties. Standard discrete and continuous probability distributions - Bernoulli, Uniform, Binomial, Poisson, Geometric, Rectangular, Exponential, Normal, Cauchy, Hypergeometric, Multinomial, Laplace, Negative binomial, Beta, Gamma, Lognormal. Random vectors, Joint and marginal distributions, conditional distributions, Distributions of functions of random variables. Modes of convergences of sequences of random variables - in distribution, in probability, with probability one and in mean square. Mathematical expectation and conditional expectation. Characteristic function, moment and probability generating functions, Inversion, uniqueness, and continuity theorems. Borel 0-1 law, Kolmogorov's 0-1 law. Tchebycheff's and Kolmogorov's inequalities. Laws of large numbers and central limit theorems for independent variables.
(ii) Statistical Methods
(a) Collection, compilation, and presentation of data, Charts, diagrams, and histograms. Frequency distribution. Measures of location, dispersion, skewness, and kurtosis. Bivariate and multivariate data. Association and contingency. Curve fitting and orthogonal polynomials. Bivariate normal distribution. regression-linear, polynomial. Distribution of the correlation coefficient, Partial and multiple correlations, Intraclass correlation, Correlation ratio.
(b) Standard errors and large sample tests. Sampling distributions of x,s2, t, chi-square, and F; tests of significance based on them, Small sample tests.
(c) Non-parametric tests-Goodness of fit, sign, median, run, Wilcoxon, Mann-Whitney, Wald-Wolfowitz, and Kolmogorov-Smirnov. Rank order statistics-minimum, maximum, range, and median. Concept of Asymptotic relative efficiency.
iii) Numerical Analysis
Finite differences of different orders: , E and D operators, factorial representation of a polynomial, separation of symbols, sub-division of intervals, differences of zero.
Concept of interpolation and extrapolation: Newton Gregory's forward and backward interpolation formulae for equal intervals, divided differences and their properties, Newton's formula for divided difference, Lagrange’s formula for unequal intervals, central difference formula due to Gauss, Sterling, and Bessel, the concept of error terms in interpolation formula.
Inverse interpolation: Different methods of inverse interpolation.
Numerical differentiation: Trapezoidal, Simpson’s one-third and three-eight rule and Waddles rule.
Summation of Series: Whose general term (i) is the first difference of a function (ii) is in geometric progression.
Numerical solutions of differential equations: Euler's Method, Milne’s Method, Picard’s Method, and Runge-Kutta Method.
(iv) Computer application and Data Processing:
Basics of Computer: Operations of a computer, Different units of a computer system like central processing unit, memory unit, arithmetic and logical unit, an input unit, output unit, etc., Hardware including different types of input, output and peripheral devices, Software, system and application software, number systems, Operating systems, packages and utilities, Low and High-level languages, Compiler, Assembler, Memory – RAM, ROM, unit of computer memory (bits, bytes, etc.), Network – LAN, WAN, internet, intranet, basics of computer security, virus, antivirus, firewall, spyware, malware, etc.
Basics of Programming: Algorithm, Flowchart, Data, Information, Database, an overview of different programming languages, frontend and backend of a project, variables, control structures, arrays, and their usages, functions, modules, loops, conditional statements, exceptions, debugging and related concepts.
STATISTICS- II (OBJECTIVE TYPE)
i) Linear Models
Theory of linear estimation, Gauss - Markov linear models, estimable functions, error and estimation space, normal equations and least square estimators, estimation of error 14 variances, estimation with correlated observations, properties of least square estimators, the generalized inverse of a matrix, and solution of normal equations, variances, and covariances of least square estimators.
(ii) Statistical Inference and Hypothesis Testing:
Characteristics of the good estimator. Estimation methods of maximum likelihood, minimum chi-square, moments, and least squares. Optimal properties of maximum likelihood estimators. Minimum variance unbiased estimators. Minimum variance bound estimators.
Cramer-Rao inequality. Bhattacharya bounds. Sufficient estimator. factorization theorem. Complete statistics. Rao-Blackwell theorem. Confidence interval estimation. Optimum confidence bounds. Resampling, Bootstrap, and Jackknife.
Hypothesis testing: Simple and composite hypotheses. Two kinds of error. Critical region. Different types of critical regions and similar regions. Power function. Most powerful and uniformly most powerful tests. Neyman-Pearson fundamental lemma. Unbiased test. Randomized test. Likelihood ratio test. Wald's SPRT, OC, and ASN functions. Elements of decision theory.
(iii) Official Statistics:
National and International official statistical system
Official Statistics: (a) Need, Uses, Users, Reliability, Relevance, Limitations, Transparency, its visibility (b) Compilation, Collection, Processing, Analysis and Dissemination, Agencies Involved, Methods
National Statistical Organization: Vision and Mission, NSSO and CSO; roles and responsibilities; Important activities, Publications, etc.
National Statistical Commission: Need, Constitution, its role, functions etc; Legal Acts/ Provisions/ Support for Official Statistics; Important Acts
Index Numbers: Different Types, Need, Data Collection Mechanism, Periodicity, Agencies Involved, Uses
Sector Wise Statistics: Agriculture, Health, Education, Women, and Child, etc. Important Surveys & Census, Indicators, Agencies, and Usages, etc.
National Accounts: Definition, Basic Concepts; issues; the Strategy, Collection of Data, and Release.
Population Census: Need, Data Collected, Periodicity, Methods of data collection, dissemination, Agencies involved.
Misc: Socio-Economic Indicators, Gender Awareness/Statistics, Important Surveys, and Censuses.
STATISTICS- III (DESCRIPTIVE TYPE)
i) Sampling Techniques
Concept of population and sample, need for sampling, complete enumeration versus sampling, basic concepts in sampling, sampling and Non-sampling error, Methodologies in sample surveys (questionnaires, sampling design, and methods followed in field investigation) by NSSO.
Subjective or purposive sampling, probability sampling or random sampling, simple random sampling with and without replacement, estimation of population mean, population proportions, and their standard errors. Stratified random sampling, proportional and optimum allocation, comparison with simple random sampling for fixed sample size. Covariance and Variance Function.
Ratio, product and regression methods of estimation, estimation of population mean, evaluation of Bias, and Variance to the first order of approximation, comparison with simple random sampling. Systematic sampling (when population size (N) is an integer multiple of sampling size (n)). Estimation of population mean and standard error of this estimate, comparison with simple random sampling.
Sampling with probability proportional to size (with and without replacement method), Des Raj and Das estimators for n=2, Horvitz-Thomson’s estimator Equal size cluster sampling: estimators of population mean and total and their standard errors, comparison of cluster sampling with SRS in terms of the intra-class correlation coefficient.
Concept of multistage sampling and its application, two-stage sampling with an equal number of second stage units, estimation of population mean, and total.Double sampling in ratio and regression methods of estimation.
Concept of Interpenetrating sub-sampling.
(ii) Econometrics:
Nature of econometrics, the general linear model (GLM) and its extensions, ordinary least squares (OLS) estimation and prediction, generalized least squares (GLS) estimation and prediction, heteroscedastic disturbances, pure and mixed estimation. Autocorrelation, its consequences, and tests. Theil BLUS procedure, estimation, and prediction, multi-collinearity problem, its implications, and tools for handling the problem, ridge regression.
Linear regression and stochastic regression, instrumental variable estimation, errors in variables, autoregressive linear regression, lagged variables, distributed lag models, estimation of lags by OLS method, Koyck’s geometric lag model.
Simultaneous linear equations model and its generalization, identification problem, restrictions on structural parameters, rank and order conditions.
Estimation in simultaneous equations model, recursive systems, 2 SLS estimators, limited information estimators, k-class estimators, 3 SLS estimators, full information maximum likelihood method, prediction, and simultaneous confidence intervals.
(iii) Applied Statistics:
Index Numbers: Price relatives and quantity or volume relatives, Link and chain relatives composition of index numbers; Laspeyre's, Paasche's’, Marshal Edgeworth and Fisher index numbers; chain base index number, tests for index number, Construction of index numbers of wholesale and consumer prices, Income distribution-Pareto, and Engel curves, Concentration curve, Methods of estimating national income, Inter-sectoral flows, Interindustry table, Role of CSO. Demand Analysis
Time Series Analysis: Economic time series, different components, illustration, additive and multiplicative models, determination of trend, seasonal and cyclical fluctuations. Time-series as discrete parameter stochastic process, autocovariance and autocorrelation functions, and their properties.
Exploratory time Series analysis, tests for trend and seasonality, exponential and moving average smoothing. Holt and Winters smoothing, forecasting based on smoothing. A detailed study of the stationary processes: (1) moving average (MA), (2) autoregressive (AR), (3) ARMA, and (4) AR integrated MA (ARIMA) models. Box-Jenkins models, choice of AR, and MA periods.
Discussion (without proof) of estimation of mean, autocovariance, and autocorrelation functions under large sample theory, estimation of ARIMA model parameters. Spectral analysis of the weakly stationary process, periodogram and correlogram analyses, computations based on Fourier transform.
STATISTICS-IV (DESCRIPTIVE TYPE)
(Equal number of questions i.e. 50% weightage from all the subsections below and candidates have to choose any two subsections and answer)
(i) Stochastic Processes
Specifications of a Stochastic Process, Markov chains, classification of states, limiting probabilities; stationary distribution; Random walk and Gambler's ruin problem. Poisson process, Birth and death process; applications to Queues-M/M/I and M/M/C models. Branching Process.
(i) Operations Research and Reliability:
Definition and Scope of Operations Research: phases in Operation Research, models and their solutions, decision-making under uncertainty and risk, use of different criteria, sensitivity analysis.
Transportation and assignment problems. Bellman’s principle of optimality, general formulation, computational methods, and application of dynamic programming to LPP. Decision-making in the face of competition, two-person games, pure and mixed strategies, the existence of solution and uniqueness of value in zero-sum games, finding solutions in 2x2, 2xm, and mxn games.
Analytical structure of inventory problems, EOQ formula of Harris, its sensitivity analysis, and extensions allowing quantity discounts and shortages. Multi-item inventory subject to constraints. Models with random demand, the static risk model. P and Q- systems with constant and random lead times.
Queuing models – specification and effectiveness measures. Steady-state solutions of M/M/1 and M/M/c models with associated distributions of queue-length and waiting time. M/G/1 queue and Pollazcek-Khinchine result. Sequencing and scheduling problems. 2-machine n-job and 3-machine n-job problems with identical machine sequence for all jobs
Branch and Bound method for solving traveling salesman problem.
Replacement problems – Block and age replacement policies.
PERT and CPM – basic concepts. Probability of project completion.
Reliability concepts and measures, components and systems, coherent systems, reliability of coherent systems.
Life-distributions, reliability function, hazard rate, common univariate life distributions – exponential, Weibull, gamma, etc. Bivariate exponential distributions. Estimation of parameters and tests in these models.
Notions of aging – IFR, IFRA, NBU, DMRL, and NBUE classes and their duals. Loss of memory property of the exponential distribution.
Reliability estimation based on failure times in variously censored life-tests and in tests with the replacement of failed items. Stress-strength reliability and its estimation.
(ii) Demography and Vital Statistics:
Sources of demographic data, census, registration, ad-hoc surveys, Hospital records, Demographic profiles of the Indian Census.
Complete life table and its main features, Uses of life table. Markham's and Gompertz curves. National life tables. UN model life tables. Abridged life tables. Stable and stationary populations.
Measurement of Fertility: Crude birth rate, General fertility rate, Age-specific birth rate, Total fertility rate, Gross reproduction rate, Net reproduction rate.
Measurement of Mortality: Crude death rate, Standardized death rates, Age-specific death rates, Infant Mortality rate, the Death rate by cause.
Internal migration and its measurement, migration models, the concept of international migration. Net migration. International and postcensal estimates. Projection method including logistic curve fitting. Decennial population census in India.
(iii) Survival Analysis and Clinical Trial:
Concept of time, order and random censoring, likelihood in the distributions – exponential, gamma, Weibull, lognormal, Pareto, Linear failure rate, inference for this distribution. Life tables, failure rate, mean residual life, and their elementary classes and their properties.
Estimation of survival function – actuarial estimator, Kaplan – Meier estimator, estimation under the assumption of IFR/DFR, tests of exponentiality against non-parametric classes, total time on the test.
Two sample problem – Gehan test, log-rank test.
Semi-parametric regression for failure rate – Cox’s proportional hazards model with one and several covariates, rank test for the regression coefficient.
Competing risk model, parametric and non-parametric inference for this model.
Introduction to clinical trials: the need and ethics of clinical trials, bias, and random error in clinical studies, the conduct of clinical trials, an overview of Phase I – IV trials, multicenter trials.
Data management: data definitions, case report forms, database design, data collection systems for good clinical practice.
Design of clinical trials: parallel vs. cross-over designs, cross-sectional vs. longitudinal designs, review of factorial designs, objectives, and endpoints of clinical trials, design of Phase I trials, design of single-stage and multi-stage Phase II trials, design and monitoring of phase III trials with sequential stopping,
Reporting and analysis: analysis of categorical outcomes from Phase I – III trials, analysis of survival data from clinical trials.
(iv) Quality Control:
Statistical process and product control: Quality of a product, need for quality control, the basic concept of process control, process capability, and product control, general theory of control charts, causes of variation in quality, control limits, sub grouping summary of out of control criteria, charts for attributes p chart, np chart, c-chart, V chart, charts for variables: R, ( X, R), ( X,σ) charts.
Basic concepts of process monitoring and control; process capability and process optimization. General theory and review of control charts for attribute and variable data; O.C. and A.R.L. of control charts; control by gauging; moving average and exponentially weighted moving average charts; Cu-Sum charts using V-masks and decision intervals; Economic design of X-bar chart.
Acceptance sampling plans for attributes inspection; single and double sampling plans and their properties; plans for inspection by variables for one-sided and two-sided specifications.
(v) Multivariate Analysis:
Multivariate normal distribution and its properties. Random sampling from a multivariate normal distribution. Maximum likelihood estimators of parameters, distribution of the sample mean vector.
Wishart matrix – its distribution and properties, distribution of sample generalized variance, null and non-null distribution of multiple correlation coefficients.
Hotelling’s T2 and its sampling distribution, application in test on mean vector for one and more multivariate normal population, and also on equality of components of a mean vector in the multivariate normal population.
Classification problem: Standards of good classification, the procedure of classification based on multivariate normal distributions.
Principal components, dimension reduction, canonical variates, and canonical correlation — definition, use, estimation, and computation.
(vi) Design and Analysis of Experiments:
Analysis of variance for one-way and two-way classifications Need for the design of experiments, a basic principle of experimental design (randomization, replication, and local control), complete analysis and layout of the completely randomized design, randomized block design and Latin square design, Missing plot technique. Split Plot Design and Strip Plot Design.
Factorial experiments and confounding in 2n and 3n experiments. Analysis of covariance. Analysis of non-orthogonal data. Analysis of missing data.
(vii) Computing with C and R :
Basics of C: Components of C language, the structure of a C program, Data type, basic data types, Enumerated data types, Derived data types, variable declaration, Local, Global, Parametric variables, Assignment of Variables, Numeric, Character, Real and String constants, Arithmetic, Relation and Logical operators, Assignment operators, Increment and decrement operators, conditional operators, Bitwise operators, Type modifiers and expressions, writing and interpreting expressions, using expressions in statements. Basic input/output.
Control statements: conditional statements, if-else, nesting of if-else, else if ladder, switch statements, loops in c, for, while do-while loops, break, continue, exit ( ), goto and label declarations, One dimensional two dimensional and multidimensional arrays. Storage classes: Automatic variables, External variables, Static variables, Scope, and a lifetime of declarations.
Functions: classification of functions, functions definition and declaration, assessing a function, return statement, parameter passing in functions. Pointers (concept only).
Structure: Definition and declaration; structure (initialization) comparison of structure variable; Array of structures: array within structures, structures within structures, passing structures to functions; Unions accessing a union member, the union of structure, initialization of a union variable, uses of the union. Introduction to a linked list, linearly linked list, insertion of a node in the list, removal of a node from the list.
Files in C: Defining and opening a file, input-output operation on a file, creating a file, reading a file. Statistics Methods and techniques in R.
The candidates should note that no request for change of center will be entertained. All the examination centers for the examination will cater to the examination for Persons with Benchmark Disabilities also. Candidates check the list of exam centers given in the table below:
|
Ahmedabad |
Bengaluru |
|
Bhopal |
Chandigarh |
|
Chennai |
Cuttack |
|
Delhi |
Dispur |
|
Hyderabad |
Jaipur |
|
Jammu |
Kolkata |
|
Lucknow |
Mumbai |
|
Patna |
Prayagraj (Allahabad) |
|
Shillong |
Shimla |
|
Thiruvananthapuram |
|
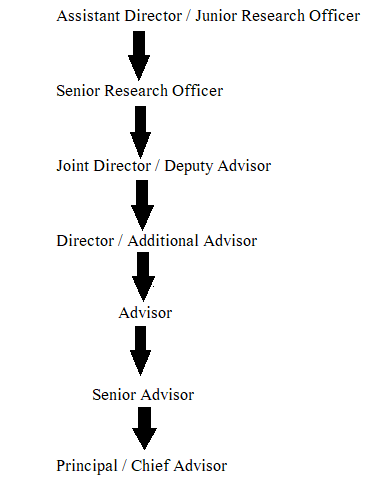
As we all know that the salary differs from the designation and posting. The in-hand salary of a Statistical Service officer is INR 59,750 - 56,100 per month. Here is a tabular for detailed salary structure as per the designation of the officers:
|
Grade/ Designation |
Pay Structure |
Strength |
|
Higher Administrative Grade + (HAG +)/ Principal Adviser (Apex) |
INR 80,000 (fixed) |
5 |
|
Higher Administrative Grade (HAG)/ Senior Economic Adviser/ Senior Adviser |
INR 67,000- (annual increment @3%) - 79,000 |
15 |
|
Senior Administrative Grade (SAG)/ Economic Adviser/ Adviser |
INR 37,400-67,000 plus Grade Pay: 10,000 |
89 |
|
Junior Administrative Grade (JAG)/ Joint Director/ Deputy Economic Adviser |
INR 15,600-39,100 plus Grade Pay: 7,600 |
148 |
|
{including Non-Functional Selection Grade (NFSG)/ Director/ Additional Economic Adviser} |
INR 37,400 - 67,000 plus Grade Pay: 8,700} |
148 |
|
Senior Time Scale (STS)/ Deputy Director/ Assistant Economic Adviser/ Senior Research Officer |
INR 15,600 - 39,100 plus Grade Pay: 6,600 |
114 |
|
Junior Time Scale (JTS)/ Assistant Director/ Research Officer |
INR 15,600 - 39,100 plus Grade Pay: 5,400 |
107 |
The Economic Service officers / Statistical Officers along with a handsome salary will be able to exercise the below-mentioned allowances: