This exam has total 80 questions and you have given 45 minutes to complete the exam.
This exam has total 2 sections.
Numerical Ability- This section has total 40 questions.
There is +1 marks for each correct answer.
And 0.00 marks will be deducted for each incorrect/wrong answer.
Reasoning Ability- This section has total 40 questions.
There is +1 marks for each correct answer.
And 0.00 marks will be deducted for each incorrect/wrong answer.
Instructions for individual section is given at the top of each section.
You have two modes of taking the exam.
Preparation mode- This mode allows you to view answers at the time you are taking an exam.
Exam mode- This mode does not allow you to view answers at the time you are taking an exam, however you can see answers once you have finished the exam.
A timer will start and will continue till exam duration.
You can see result and solved exam by clicking "View Result" button
You can see your correct/incorrect answers by clicking "View Solved Exam" button in result popup
Numerical Ability
Question 1.
A 1.6 m tall observer is 45 meters away from a tower. The angle of elevation from his eye to the top of the tower is 30°, then the height of the tower in meters is
1.6 मीटर लंबा प्रेक्षक एक टॉवर से 45 मीटर दूर है। टॉवर के शीर्ष पर उसकी आंख से ऊंचाई का कोण 30 ° है, फिर मीटर में टॉवर की ऊंचाई है?
A.
B.
C.
D.
Answer
C
Explanation
BC=45 m
AB=h m
Tan 30=AB/BC
1/√3=h/45
h=45/√3
h=45/1.732
h=25.98 m
AD=AB+BD
AD=25.98+1.6
AD=27.58 m
So the correct answer is option C.
BC=45 m
AB=h m
Tan 30=AB/BC
1/√3=h/45
h=45/√3
h=45/1.732
h=25.98 m
AD=AB+BD
AD=25.98+1.6
AD=27.58 m
इसलिए सही उत्तर विकल्प C है।
Question 2.
70% of 20% of 240 = ?
240 के 70% का 20% =?
A.
B.
C.
D.
Answer
D
Explanation
240 * 70/100 * 20/100=33.6
So the correct answer is option D.
240 * 70/100 * 20/100=33.6
इसलिए सही उत्तर विकल्प D है l
Question 3.
There is a road besides a river. Two friends Ram & Shyam started their journey from place P, moved to the garden located at another place Q & then returned to place P. Ram moves by swimming at a speed of 15 km/hr while Shyam sails on a boat at a speed of about 12 km/hr. If the flow of water current is at the speed of 6 km/hr, what will be the average speed of boat sailor?
एक नदी के बगल में एक सड़क है। दो दोस्त राम और श्याम ने P से अपनी यात्रा शुरू की, एक अन्य स्थान Q पर स्थित बगीचे में चले गए और फिर P पर वापस आये । राम 15 किमी / घंटा की गति से तैरकर वापस आ गया , जबकि श्याम लगभग 12 किमी / घंटा की गति से नाव पर बैठकर वापस आता है । यदि जल प्रवाह की गति 6 किमी / घंटा की है, तो नाविक की औसत गति क्या होगी?
A.
B.
C.
D.
Answer
B
Explanation
Shyam sails on a boat at a speed of about 12 km/hr.
The speed of current=6 km/hr
The downstream speed of Shyam=12+6=18 km/hr
The upstream speed of Shayam=12-6=6 km/hr
So the average speed of Shyam(boat sailor)=2 x 18 x 6/18+6
=9 km/hr
So the correct answer is option B.
श्याम नाव पर लगभग 12 किमी / घंटा की गति से नाव चलाता है।
धारा की गति = 6 किमी / घंटा
श्याम की धारा की दिशा में गति = 12 + 6 = 18 किमी / घंटा
श्याम की धारा के विपरीत गति = 12-6 = 6 किमी / घंटा
अतः श्याम की औसत गति ( नाविक) = 2 x 18 x 6/18 + 6
= 9 किमी / घंटा
इसलिए सही उत्तर विकल्प B है।
Question 4.
How many seconds will a 500-meter long train take to cross a man walking with a speed of 3 km/hr in the direction of the moving train if the speed of the train is 63 km/hr?
500 मीटर लंबी ट्रेन, चलती हुई ट्रेन की दिशा में 3 किमी/घंटा की गति से चल रहे एक व्यक्ति को पार करने में कितने सेकंड का समय लेगी, यदि ट्रेन की गति 63 किमी/घंटा है?
A.
B.
C.
D.
Answer
B
Explanation
Length of the train = 500 m
Speed of the train = 63 km/hr
Speed of the man = 3 km/hr
Relative speed = 63-3 km/hr = 60 km/hr = 60*5/18 m/s
Time = ?
Speed = Distance/Time
60*5/18 = 500/t
T = 500*18/60*5
T = 100*3/10 = 30 sec
So the train will cross the man in 30 sec.
So the correct answer is option B.
ट्रेन की लंबाई = 500 मी
ट्रेन की चाल = 63 किमी/घंटा
आदमी की चाल = 3 किमी/घंटा
सापेक्ष चाल = 63-3 किमी/घंटा = 60 किमी/घंटा = 60*5/18 मीटर/सेकेंड
समय = ?
चाल = दूरी/समय
60*5/18 = 500/t
T = 500*18/60*5
T = 100*3/10 = 30 सेकंड
अतः ट्रेन 30 सेकंड में आदमी को पार करेगी।
इसलिए सही उत्तर विकल्प B है l
Question 5.
A man completes a journey in 10 hours. He travels the first half of the journey at the rate of 21 km/hr and the second half at the rate of 24 km/hr. Find the total journey in km.
एक आदमी 10 घंटे में एक यात्रा पूरी करता है। वह यात्रा के पहले भाग को 21 किमी/घंटा की गति से और दूसरे भाग को 24 किमी/घंटा की गति से तय करता है। किमी में कुल यात्रा ज्ञात कीजिए।
A.
B.
C.
D.
Answer
B
Explanation
Let the total journey is x+x = 2x km.
He travels the first half of the journey at the rate of 21 km/hr. Then the time to complete the first half = Distance/Speed = x/21 hr
He travels the second half of the journey at the rate of 24 km/hr. Then the time to complete the second half = x/24 hr
Given total time is 10 hr. Then -
time to complete the first half+time to complete the second half = total time
x/21 + x/24 = 10
24x+21x/21*24 = 10
24x+21x = 21*24*10
45x = 5040
x = 112
Hence the total journey = 2x = 112*2 = 224 km.
So the correct answer is option B.
माना कि कुल यात्रा x+x = 2x किमी है।
वह यात्रा के पहले भाग को 21 किमी/घंटा की गति से तय करता है। अतः पहले भाग को पूरा करने में लगा समय = दूरी/गति = x/21 घंटा
वह यात्रा के दूसरे भाग को 24 किमी/घंटा की गति से तय करता है। अतः दूसरे भाग को पूरा करने में लगा समय = x/24 घंटा
दिया गया है -
कुल समय 10 घंटे है। अतः -
पहले भाग को पूरा करने में लगा समय + दूसरी भाग को पूरा करने में लगा समय = कुल समय
x/21 + x/24 = 10
24x+21x/21*24 = 10
24x+21x = 21*24*10
45x = 5040
x = 112 km
अत: कुल यात्रा = 2x = 112*2 = 224 किमी.
इसलिए सही उत्तर विकल्प B है।
Question 6.
A is 20% more efficient than B. How much time will they work together to complete a job that B alone could have done in 22 days?
A, की क्षमता B से 20% अधिक है। वे एक साथ कार्य करते हुए उस कार्य को पूरा करने में कितना समय लेंगे जिसे B अकेले 22 दिनों में पूरा कर सकता था?
A.
B.
C.
D.
Answer
B
Explanation
Given - A is 20% more efficient than B.
Efficiency - A B
120% 100%
6 5
Time taken - 5 6 (Time is opposite of Efficiency)
Let A and B can do a work in 5x and 6x days respectively.
Given -
B can do the work in 22 days then -
6x = 22
x = 22/6 = 11/3
A can do the work in 5x days then = 5*11/3 = 55/3 days
1 day work of A = 3/55
1 day work of A+B = 1 days work of A + 1 day work of B
= 3/55 + 1/22
= 6+5/110
= 11/110
= 1/10
Hence A and B can do the work together in 10 days.
So the correct answer is option B.
दिया गया है - A, की क्षमता B से 20% अधिक है।
क्षमता - A B
120% 100%
6 5
लिया गया समय - 5 6 (समय क्षमता के विपरीत होता है)
माना A और B एक काम को क्रमशः 5x और 6x दिनों में कर सकते हैं।
दिया गया -
B उस काम को 22 दिनों में कर सकता है तो -
6x = 22
x = 22/6 = 11/3
A उस काम को 5x दिनों में कर सकता है तो = 5*11/3 = 55/3 दिन
A का 1 दिन का कार्य = 3/55
A+B का 1 दिन का कार्य = A का 1 दिन का कार्य + B का 1 दिन का कार्य
= 3/55 + 1/22
= 6+5/110
= 11/110
= 1/10
अत: A और B मिलकर उस कार्य को 10 दिनों में कर सकते हैं।
इसलिए सही उत्तर विकल्प B है।
Question 7.
Which of the following fraction is the smallest?
निम्नलिखित में से कौन सा अंश सबसे छोटा है?
A.
B.
C.
D.
Answer
B
Explanation
13/16=0.8125
13/19=0.6842
17/21=0.809
7/8=0.875
So the correct answer is option B.
13/16=0.8125
13/19=0.6842
17/21=0.809
7/8=0.875
इसलिए सही उत्तर विकल्प B है।
Question 8.
A number x when divided by 289 leave 18 as the remainder. The same number when divided by 17 leaves y as a remainder. the value of y is :
एक संख्या x को जब 289 से विभाजित किया जाता है तो 18 शेषफल आता है। इसी संख्या को जब 17 से विभाजित किया जाता है तो y शेष आता है। y का मान है:
A.
B.
C.
D.
Answer
D
Explanation
In such a question which gives remainder and asks for new reminder. There is an easy method to get new reminders.
Old remainder / new divider = New reminder
Old remainder=18
New divider=17
New reminder = 18/17
=1
So the correct answer is option D.
ऐसे प्रश्न जिसमे शेष दिया रहता है और नए शेषफल के लिए पूछता है। नया शेषफल प्राप्त करने की एक आसान विधि है।
पुराना शेषफल / नया विभाजक = नया शेषफल
पुराना शेष = 18
नवीन विभक्त = 17
नया अनुस्मारक = 18/17
= 1
इसलिए सही उत्तर विकल्प D है।
Question 9.
Gauri went to the stationers and bought things worth Rs. 25, out of which 30 paise went on sales tax on taxable purchases. If the tax rate was 6%, then what was the cost of the tax free items?
गौरी ने स्टेशनर्स के पास जाकर 25 रुपये की चीजें खरीदीं, जिसमें से 30 पैसे कर योग्य खरीद पर बिक्री कर पर गए। यदि कर की दर 6% थी, तो कर मुक्त वस्तुओं की कीमत क्या थी?
A.
B.
C.
D.
Answer
C
Explanation
Let the amount taxable purchases be Rs. x.
Then, 6% of x =30/100
(30/100) *(100/6)=5
So cost of tax free items = Rs. [25 - (5 + 0.30)] = Rs. 19.70
So the correct answer is option
माना कि कर योग्य खरीद x रु है l
फिर, x का 6% = 30/100
(30/100) * (100/6) = 5
इसलिए कर मुक्त वस्तुओं की कीमत = [25 - (5 + 0.30)] रु = 19.70 रु।
इसलिए सही उत्तर विकल्प C है l
Question 10.
How much time will it take for an amount of Rs. 450 to yield Rs. 81 as interest at 4.5% per annum of simple interest?
450 रुपये की राशि का साधारण ब्याज से 4.5% प्रति वर्ष की दर से ब्याज के रूप में 81 रुपये प्राप्त करने में कितना समय लगेगा?
A.
B.
C.
D.
Answer
B
Explanation
Principal (P) = 450 Rs
Simple Interest (SI) = 81 Rs
Rate (r) = 4.5%
Time (t) = ?
Formula -
Simple Interest = P*r*t/100
81 = 450*4.5*t/100
t = 81*100/450*4.5
t = 4 years
Hence it will take 4 years for an amount of Rs. 450 to yield Rs. 81 as interest at 4.5% per annum.
So the correct answer is option B.
मूलधन (P) = 450 रुपये
साधारण ब्याज (SI) = 81 रुपये
दर (r) = 4.5%
समय (t) = ?
साधारण ब्याज =P*r*t/100
81 = 450*4.5*t/100
t = 81*100/450*4.5
t = 4 वर्ष
अतः 450 रुपये की राशि पर 81 रुपये प्रति वर्ष 4.5% की दर से ब्याज के रूप में प्राप्त करने में 4 वर्ष लगेंगे।
इसलिए सही उत्तर विकल्प B है।
Question 11.
A library has an average of 510 visitors on Sundays and 240 on other day. The average number of visitors in a month of 30 days starting with sunday is
एक पुस्तकालय में रविवार को औसतन 510 दर्शक और दूसरे दिन 240 होते हैं। 30 दिनों के रविवार से शुरू होने वाले एक महीने में दर्शकों की औसत संख्या है:
A.
B.
C.
D.
Answer
B
Explanation
As the month begin with sunday, so there will be five sundays in the month -
So the number of visitor on sunday = 510 x 5
Remaining days = 25 days
So the number of visitor in 25 days = 240 x 25
So the average number of visitor in 30 days -
510x5 + 240x25 / 30
=8550/30
=285
So the correct answer is option B.
जैसा कि महीने की शुरुआत रविवार से होती है, इसलिए महीने में पांच रविवार होंगे -
अतः रविवार को दर्शको की संख्या = 510 x 5
शेष दिन = 25 दिन
तो 25 दिनों में दर्शकों की संख्या = 240 x 25
तो 30 दिनों में दर्शकों की औसत संख्या -
510x5 + 240x25 / 30
= 8550/30
= 285
इसलिए सही उत्तर विकल्प B है।
Question 12.
A solid metallic sphere of radius 14 cm is melted and recast into a cone with diameter of the base as 14 cm. What is the height (in cm) of the cone?
14 सेमी त्रिज्या का एक ठोस धातु का गोला पिघलाया जाता है और 14 सेमी आधार के व्यास वाले एक शंकु में पुनर्गठित किया जाता है। शंकु की ऊंचाई (सेमी में) क्या है?
A.
B.
C.
D.
Answer
D
Explanation
Radius of sphere(r)=14 cm
The diameter of cone(d)=14 cm
The Radius of cone(R)=14/2=7 cm
Height of cone(h)=?
A solid metallic sphere is melted and recast into a cone so -
The volume of Sphere=The volume of Cone
4x22/7x(r)^3=22/7x(R)^2 x h
4x(14)^3=(7)^2 x h
4x14x14x14/7x7=h
h=4x2x2x14
h=224 cm
So the correct answer is option D.
गोले की त्रिज्या (r) = 14 सेमी
शंकु का व्यास (d) = 14 सेमी
शंकु की त्रिज्या (R) = 14/2 = 7 सेमी
शंकु की ऊँचाई (h) =?
एक ठोस धातु का गोला पिघलाया जाता है और शंकु में बदल जाता है -
गोले का आयतन = शंकु का आयतन
4x22 / 7x (r)^3 = 22 / 7x (R) ^ 2 x h
4x (14)^3 = (7)^2 x h
4x14x14x14 / 7x7 = h
h = 4x2x2x14
h= 224 सेमी
इसलिए सही उत्तर विकल्प D है।
Question 13.
0.04 x 0.0162 is equal to:
0.04 x 0.0162 के बराबर है:
A.
B.
C.
D.
Answer
B
Explanation
0.04 x 0.0162
=4 x 10^-2 x 162 x 10^-4
=648 x 10^-6
=6.48 x 10^-4
So the correct answer is option B
0.04 x 0.0162
=4 x 10^-2 x 162 x 10^-4
=648 x 10^-6
=6.48 x 10^-4
इसलिए सही उत्तर विकल्प B है।
Question 14.
LCM of two numbers is 2079 and their HCF is 27. If one of the numbers is 189, find the other
दो संख्याओं का लघुत्तम समापवर्तक 2079 है और उनका म.स. 27 है। यदि संख्याओं में से एक संख्या 189 है, तो दूसरी संख्या ज्ञात कीजिए।
A.
B.
C.
D.
Answer
A
Explanation
LCM =2079
HCF = 27
First number =189
Let the Second number =x
Formula used -
Product of two number = LCM*HCF
First number*second number = LCM*HCF
2079*27 = 189*x
x= 2079*27/189
x = 297
So the other number is 297.
Hence the correct answer is option A.
LCM =2079
HCF = 27
पहली संख्या = 189
माना दूसरी संख्या =x
प्रयुक्त सूत्र -
संख्याओं का गुणनफल = ल.स.*म.स.
पहली संख्या*दूसरी संख्या = ल.स.*म.स.
2079*27 = 189*x
x = 2079*27/189
x = 297
दूसरी संख्या 297 है।
अतः सही उत्तर विकल्प A है।
Question 15.
The ratio of the first and second-class fares between the two stations is 6 : 4 and the number of passengers travelling by first and second-class is 1 : 30. If Rs. 2100 is collected as fare, what is the amount collected from first class passengers.
दो स्टेशनों के बीच प्रथम और द्वितीय श्रेणी के किराए का अनुपात 6: 4 है और प्रथम और द्वितीय श्रेणी के यात्रियों की संख्या 1: 30 है। 2100 किराया के रूप में एकत्र किया जाता है, प्रथम श्रेणी के यात्रियों से क्या राशि एकत्र की जाती है l
A.
B.
C.
D.
Answer
A
Explanation
First class Second class
Fare 6x : 4x
Passengers 1 : 30
Total fare = 6x : 120x
=x:20x=21x
=21x=2100
x=100
The amount collection from 1st class passenger = (2100 x 1/21) = Rs.100
So the correct answer is option A.
प्रथम श्रेणी द्वितीय श्रेणी
किराया 6x : 4x
यात्री 1 : 30
कुल किराया = 6x: 120x
= x: 20x = 21x
= 21x = 2100
x = 100
प्रथम श्रेणी के यात्री से राशि संग्रह = (2100 x 1/21) = Rs.100
इसलिए सही उत्तर विकल्प A है।
Question 16.
what is the simplified value of Sin 2A/1+Cos 2A
Sin 2A/1+Cos 2A का मान क्या होगा?
A.
B.
C.
D.
Answer
A
Explanation
Sin 2A/1+Cos 2A
=2 sinaA.cosA/1+2cos^2A-1
=sinA/cosA
=tanA
So the correct answer is option A.
Sin 2A/1+Cos 2A
=2 sinaA.cosA/1+2cos^2A-1
=sinA/cosA
=tanA
इसलिए सही उत्तर विकल्प A है।
Question 17.
A person borrows Rs. 5000 for 2 years at 4% p.a. simple interest. He immediately lends it to another person at 6 1/4% p.a for 2 years. Find his gain in the transaction per year.
एक व्यक्ति 4% साधारण ब्याज पर 2 वर्ष के लिए 5000 रु उधार लेता है। वह इसे तुरंत किसी अन्य व्यक्ति को 6 1/4% प्रति वर्ष की दर से 2 वर्ष के लिए उधार देता है। प्रति वर्ष लेन-देन में उसका लाभ ज्ञात कीजिए।
A.
B.
C.
D.
Answer
A
Explanation
A person borrows Rs. 5000 for 2 years at 4% p.a. simple interest.
Principal = 5000 Rs
Time = 2 years
Rate = 4%
Simple Interest = P*r*t/100
SI = 5000*4*2/100
SI = 400 Rs.
He immediately lends it to another person at 6% p.a for 2 years.
Now -
Principal = 5000 Rs
Rate = 6%
Time = 2 years
Simple Interest = P*r*t/100
SI = 5000*6*2/100
SI = 625 Rs
Gain in 2 years = 625 - 400 = 225
Gain in 1 year = 225/2 = 112.5 Rs
So the correct answer is option A.
एक व्यक्ति 4% साधारण ब्याज पर 2 वर्ष के लिए 5000 रु उधार लेता है।
मूलधन = 5000 रुपये
समय = 2 वर्ष
दर = 4%
साधारण ब्याज = P*r*t/100
SI = 5000*4*2/100
SI = 400 रुपये
वह इसे तुरंत किसी अन्य व्यक्ति को 6% प्रति वर्ष की दर से 2 वर्ष के लिए उधार देता है।
अब -
मूलधन = 5000 रुपये
दर = 6%
समय = 2 वर्ष
साधारण ब्याज = P*r*t/100
SI = 5000*6*2/100
SI = 625 रुपये
2 वर्षों में लाभ = 625 - 400 = 225
1 वर्ष में लाभ = 225/2 = 112.5 रुपये
इसलिए सही उत्तर विकल्प A है।
Question 18.
If x/4 – (x – 3)/5 = 1, then find the value of x.
यदि x / 4 - (x - 3) / 5 = 1 है, तो x का मान ज्ञात कीजिए।
A.
B.
C.
D.
Answer
C
Explanation
x/4 – (x – 3)/5 = 1
5x-4x+12 / 20=1
x+12=20
x=8
So the correct answer is option C
x/4 – (x – 3)/5 = 1
5x-4x+12 / 20=1
x+12=20
x=8
इसलिए सही उत्तर विकल्प C है।
Question 19.
If a person walks at 14 km/hr instead of 10 km/hr, he would have walked 20 km more. The actual distance travelled by him is:
यदि कोई व्यक्ति 10 किमी / घंटा के बजाय 14 किमी / घंटा की गति से चलता है, तो वह 20 किमी अधिक चल सकता है। उनके द्वारा यात्रा की गई वास्तविक दूरी है:
A.
B.
C.
D.
Answer
A
Explanation
Let the actual distance=x
Time = Distance/Speed
According to the question -
x/10=x+20/14
14x=10x+200
4x=200
x=50 km
So the correct answer is option A.
माना वास्तविक दूरी = x
समय = दूरी / गति
प्रश्न के अनुसार -
x / 10 = x + 20/14
14x = 10x + 200
4x = 200
x = 50 किमी
इसलिए सही उत्तर विकल्प A है।
Question 20.
Three pipes A, B and C can fill a tank in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 7 hours. The number of hours taken by C alone to fill the tank is:
तीन पाइप A, B और C एक टंकी को 6 घंटे में भर सकते हैं। इस पर 2 घंटे एक साथ काम करने के बाद, C को बंद कर दिया जाता है और A और B शेष भाग को 7 घंटे में भर सकते हैं। टैंक को अकेले भरने में C द्वारा लिए गए घंटों की संख्या है:
A.
B.
C.
D.
Answer
C
Explanation
Pipes A, B and C can fill a tank in 6 hours.
The part of the tank filled by these three pipes in 1 hours = ⅙
These three pipes work for 2 hours.
The part filled by these three pipes in 2 hours = 2/6 = ⅓
Remaining part = 1-⅓ = ⅔
A and B can fill the remaining part in 7 hours.
A and B can fill the ⅔ part of the tank in = 7 hours
A and B can fill the tank in = 7*3/2 = 21/2
The part of the tank filled by pipes A and B in 1 hours = 1/21/2 = 2/21
The part of the tank filled by pipe C in 1 hours = The part of the tank filled by these three pipes in 1 hours - The part of the tank filled by pipes A and B in 1 hours
The part of the tank filled by pipe C in 1 hours = ⅙-2/21 = 7-4/42 = 3/42 = 1/12
Hence C can fill the the tank in 12 hours.
Hence the correct answer is option B.
पाइप A, B और C एक टैंक को 6 घंटे में भर सकते हैं।
इन तीन पाइपों द्वारा 1 घंटे में भरा गया टैंक का भाग = ⅙
ये तीनों पाइप 2 घंटे काम करते हैं।
इन तीनों पाइपों द्वारा 2 घंटे में भरा गया भाग = 2/6 = ⅓
शेष भाग = 1-⅓ = ⅔
A और B शेष भाग को 7 घंटे में भर सकते हैं।
A और B टंकी के ⅔ भाग को = 7 घंटे में भर सकते हैं l
A और B टैंक को = 7*3/2 = 21/2 घंटे में भर सकते हैं l
पाइप A और B द्वारा 1 घंटे में भरा गया टैंक का भाग = 1/21/2 = 2/21
पाइप C द्वारा 1 घंटे में भरा गया टैंक का भाग = तीन पाइपों द्वारा 1 घंटे में भरा गया टैंक का भाग - पाइप A और B द्वारा 1 घंटे में भरा गया टैंक का भाग
पाइप C द्वारा 1 घंटे में भरा गया टैंक का भाग = ⅙-2/21 = 7-4/42 = 3/42 = 1/12
अतः पाइप C टंकी को 12 घंटे में भर सकता है।
अतः सही उत्तर विकल्प B है।
Question 21.
What is the average of first 29 even numbers?
पहले 29 सम संख्याओं का औसत क्या है?
A.
B.
C.
D.
Answer
A
Explanation
Sum of first n even numbers
=n(n+1)
=29(29+1)
=870
Average =Sum/number
=870/29
=30
So the correct answer is option A.
प्रथम n सम संख्याओ का औसत
=n(n+1)
=29(29+1)
=870
औसत=योग / संख्या
=870/29
=30
इसलिए सही उत्तर विकल्प A है।
Question 22.
Which of the following has the most number of divisors?
निम्नलिखित में से किसके भाजको की संख्या सबसे अधिक है?
A.
B.
C.
D.
Answer
B
Explanation
99 = 1 × 3 × 3 × 11
101 = 1 × 101
176 = 1 × 2 × 2 × 2 × 2 × 11
182 = 1 × 2 × 7 × 13
Divisors of 99 are 1, 3, 9, 11, 33, 99
Divisors of 101 are 1 and 101
Divisors of 176 are 1, 2, 4, 8, 11, 16, 22, 44, 88 and 176
Divisors of 182 are 1, 2, 7, 13, 14, 26, 91 and 182
So 176 has the most number of divisors.
So the correct answer is option B.
99 = 1 × 3 × 3 × 11
101 = 1 × 101
176 = 1 × 2 × 2 × 2 × 2 × 11
182 = 1 × 2 × 7 × 13
99 के भाजक 1, 3, 9, 11, 33, 99 हैं
101 के भाजक 1 और 101 हैं
176 के भाजक 1, 2, 4, 8, 11, 16, 22, 44, 88 और 176 हैं
182 के भाजक 1, 2, 7, 13, 14, 26, 91 और 182 हैं
इसलिए 176 में सबसे अधिक भाजक हैं।
इसलिए सही उत्तर विकल्प B है।
Question 23.
Two trains, each 100 m long, moving in opposite directions, cross each other in 8 seconds. If one is moving twice as fast as the other, then the speed of the faster train is
दो ट्रेनें, प्रत्येक 100 मीटर लंबी, विपरीत दिशाओं में चलती हुई, 8 सेकंड में एक दूसरे को पार करती हैं। यदि एक ट्रेन दूसरे की तुलना में दुगनी गति से चल रही है, तो तेज गति वाली ट्रेन की चाल है?
A.
B.
C.
D.
Answer
C
Explanation
Length of Each train = 100 m
Total length or distance covered by train = 100+100 m = 200 m
Let the speed of slower train = x m/s
Then the speed of faster train = 2x m/s
Relative speed = 2+x+ m/s = 3x m/s
Time to cross each other = 8 sec
Speed = Distance/Time
3x = 200/8
3x = 25
X = 25/3 = 25/3 m/s
Speed of faster train = 2x = 25*2/3 m/s= 50/3 m/s= 50*18/5*3 km/hr = 10*6 km/hr = 60 km/hr.
So the correct answer is option C.
प्रत्येक ट्रेन की लंबाई = 100 मी
ट्रेन की लम्बाई या तय की गई कुल दूरी = 100+100 मीटर = 200 मीटर
माना धीमी ट्रेन की चाल = x मी/से
तब तेज गति वाली रेलगाड़ी की चाल = 2x मी/से
सापेक्ष चाल = 2+x+ मी/से = 3x मी/से
एक दूसरे को पार करने का समय = 8 सेकंड
चाल = दूरी/समय
3x = 200/8
3x = 25
x = 25/3 = 25/3 मी/से
तेज ट्रेन की चाल = 2x = 25*2/3 मी/से= 50/3 मी/से = 50*18/5*3 किमी/घंटा = 10*6 किमी/घंटा = 60 किमी/घंटा।
अतः तेज ट्रेन की गति 60 किमी/घंटा है l
इसलिए सही उत्तर विकल्प C है l
Question 24.
He marked price of a table is 50% more than its cost price. What discount percentage should be offered by the shopkeeper to sell his table at no profit or no loss?
उसने एक टेबल की कीमत उसकी लागत मूल्य से 50% अधिक बताई। दुकानदार द्वारा अपनी मेज को बिना किसी लाभ या हानि के बेचने के लिए क्या छूट प्रतिशत की पेशकश की जानी चाहिए?
A.
B.
C.
D.
Answer
B
Explanation
Let the cost price of table=100 rs
So the marked price=150 rs
If no loss & no profit, then selling price=100 rs
Let the discount price=x
So-
MP * (100-Discount%)/100=Selling price
150(100-x)/100=100
x=33.33%
So the correct answer is option B.
माना मेज की लागत मूल्य = 100 रुपये
तो चिह्नित मूल्य = 150 रुपये
यदि कोई हानि और कोई लाभ नहीं है, तो बिक्री मूल्य = 100 रुपये
माना छूट % = x
इसलिए-
MP * (100-छूट%) / 100 = बिक्री मूल्य
150 (100-x) / 100 = 100
x = 33.33%
इसलिए सही उत्तर विकल्प B है।
Question 25.
In what time will Rs.8,750 at 8% p.a simple interest will can a total interest of 6/25th of the principal?
कितने समय बाद 8,750 रू का 8% साधारण ब्याज की दर से कुल ब्याज ,मूलधन का 6/25 वा भाग होगा?
A.
B.
C.
D.
Answer
B
Explanation
Principle amount(P)=8750 rs
Rate(r)=8%
Simple Interest(SI)=P x 6/25
SI=8750 x 6/25
SI=2100 rs
Time(t)=?
SI=P x r x t/100
2100=8750 x 8 x t/100
t=2100 x 100 / 8750 x 8
t=3 year
So the correct answer is option B.
मूल राशि (P) = 8750 रू
दर (r) = 8%
साधारण ब्याज (SI) = P x 6/25
SI = 8750 x 6/25
SI = 2100 रुपये
समय (t) =?
SI = P x r x t/100
2100 = 8750 x 8 x t / 100
t = 2100 x 100 / 8750 x 8
t = 3 वर्ष
इसलिए सही उत्तर विकल्प B है।
Question 26.
Robert is travelling on his cycle and has calculated to reach point A at 2 P.M. if he travels at 10 kmph, he will reach there at 12 noon if he travels at 15 kmph. At what speed must he travel to reach A at 1 P.M.?
रॉबर्ट अपने साइकिल पर यात्रा कर रहा हैं यदि वह 10 किमी प्रति घंटे की रफ्तार से यात्रा करता है,तो वह दोपहर 2 बजे गंतव्य पर पहुचेगा ,यदि वह 15 किमी प्रति घंटे की रफ्तार से यात्रा करता है तो वह दोपहर 12 बजे वहां पहुंचेगा l पर A तक 1 बजे पहुँचने के लिए उसे किस गति से यात्रा करनी चाहिए?
A.
B.
C.
D.
Answer
B
Explanation
Let the total distance to reach the point A is x km.
Time=Distance/Speed
x/10-x/15=2
=x/30=2
=x=60 km
Time taken by Robert to cover 60 km at 10 kmph= 60/10hrs=6 hrs
So Robert started travelling 6 hrs before 2 PM means 8 AM.
Now difference between 8 am to 1 pm is 5 hrs.
The the speed of Robert to reach the point A=60/5=12kmph
So the correct answer is option B.
माना कि A तक पहुंचने के लिए कुल दूरी x किमी है।
समय = दूरी / चाल
x / 10-x/ 15 = 2
= x / 30 = 2
= x = 60 किमी
रॉबर्ट द्वारा 60 किमी को 10 किमी प्रति घंटे की चाल से कवर करने के लिए लिया गया समय= 60/10 घंटे = 6 घंटे
इसलिए राबर्ट ने 2 बजे से 6 घंटे पहले सुबह 8 बजे से पहले की यात्रा शुरू की।
अब सुबह 8 से 1 बजे के बीच का अंतर 5 घंटे है।
रॉबर्ट की गति बिंदु A तक पहुंचने के लिए= 60/5 = 12 किमी प्रति घंटे
इसलिए सही उत्तर विकल्प B है।
Question 27.
The difference of two numbers is 1365. On dividing the larger number by the smaller, we get 6 as quotient and the 15 as remainder. What is the smaller number ?
दो संख्याओं का अंतर 1365 है। छोटे द्वारा बड़ी संख्या को विभाजित करने पर, हमें 6 भागफल और 15 शेष मिलते हैं। छोटी संख्या क्या है?
A.
B.
C.
D.
Answer
B
Explanation
Let the two numbers= x,y
the difference of two numbers is 1365.
x-y=1365----(1)
On dividing the larger number by the smaller, we get 6 as quotient and the 15 as remainder so-
x=6y+15-----(2)
After solving equation (1) and (2)
y=270
So the correct answer is option B.
माना दो नंबर = x, y
दो संख्याओं का अंतर 1365 है।
x-y = 1365 ---- (1)
छोटी से बड़ी संख्या को विभाजित करने पर, हमें 6 भागफल और 15 शेष मिलते हैं अतः -
x= 6y + 15 ----- (2)
समीकरण (1) और (2) हल करने के बाद
y = 270
इसलिए सही उत्तर विकल्प B है।
Question 28.
If the radius of a circle is nine times, its perimeter will become how many times of its previous perimeter?
यदि किसी वृत्त की त्रिज्या नौ गुना है, तो उसकी परिधि उसकी पिछली परिधि के कितने गुना होगी?
A.
B.
C.
D.
Answer
A
Explanation
Let the radius of initial circle=r
Radius of new circle=9r
Perimeter of initial circle=2πr
Perimeter of new circle=2π(9r)
=18πr
So new perimeter is 9 times of previous perimeter.
So the correct answer is option A.
माना प्रारंभिक वृत्त की त्रिज्या = r
नए वृत्त की त्रिज्या = 9r
प्रारंभिक वृत्त की परिधि = 2πr
नए वृत्त की परिधि = 2π (9r)
= 18πr
तो नई परिधि पिछली परिधि का 9 गुना है।
इसलिए सही उत्तर विकल्प A है।
Question 29.
The average of the first and the second of three numbers is 15 more than the average of the second and the third of these numbers. What is the difference between the first and the third of these three numbers?
पहली और दूसरी तीन संख्याओं का औसत इन संख्याओं के दूसरे और तीसरे के औसत से 15 अधिक है। इन तीनों संख्याओं के पहले और तीसरे में क्या अंतर है?
A.
B.
C.
D.
Answer
A
Explanation
Let-
First no = x
Second no =y
Third no = z
According to question.
(x+y)/2 = 15 + (y+z)/2
Multiply above equation by 2
x + y = 30+y+z
So-
x-z = 30
The difference between first and third no is 30.
So the correct answer is option A.
माना -
पहली संख्या = x
दूसरी संख्या =y
तीसरी संख्या = z
प्रश्न के अनुसार।
(x + y) / 2 = 15 + (y + z) / 2
समीकरण को 2 से गुणा करें
x + y = 30 + y + z
इसलिए-
x-z = 30
पहली और तीसरी संख्या का अंतर 30 है।
इसलिए सही उत्तर विकल्प A है l
Question 30.
Two numbers differ by 5. If their product is 336, the sum of two number is -
दो संख्याओं का अंतर 5 हैं। यदि उनका गुणनफल 336 है, तो दो संख्याओं का योग है -
A.
B.
C.
D.
Answer
C
Explanation
Let the no = x and y
Given -
x-y = 5
xy=336
x+y = ?
Formula -
(x-y)^2 = (x+y)^2 -4xy
5^2 = (x+y)^2 - 4*336
25 = (x+y)^2 - 1344
1344+25 = (x+y)^2
1369 = (x+y)^2
x+y = 37
So the correct answer is option C.
माना संख्या = x और y
दिया हुआ है -
x-y = 5
xy = 336
x + y =?
सूत्र -
(x-y)^2 = (x+y)^2 -4xy
5^2 = (x+y)^2 - 4*336
25 = (x+y)^2 - 1344
1344+25 = (x+y)^2
1369 = (x+y)^2
x+y = 37
इसलिए सही उत्तर विकल्प C है।
Question 31.
A pipe can empty a tank in 40 min. A second pipe with diameter twice as much as that of the first is also attached with the tank to empty it. The two together can empty the tank in
एक पाइप किसी टंकी को 40 मिनट में खली करता है । दूसरा पाइप जिसका व्यास पहले पाइप से दुगुना है टैंक को खाली करने के लिए जोड़ दिया जाता है । दोनों पाइप एक साथ टैंक को कितने समय में खाली करेंगे ?
A.
B.
C.
D.
Answer
B
Explanation
A pipe can empty a tank in 40 min.
The part empty by the pipe in 1 min = 1/40
The pipe with twice the diameter can empty the tank in half time. So the second pipe can empty the tank in 20 min.
The part empty by second pipe in 1 min = 1/20
The part emptied by both the pipes in 1 min = 1/40+1/20
= 1+2/40
=3/40
So the two pipes can empty the tank together in 40/3 min = 13 ⅓ min.
Hence the correct answer is option B.
एक पाइप 40 मिनट में एक टैंक खाली कर सकता है।
1 मिनट में पाइप द्वारा खाली भाग = 1/40
दुगुना व्यास वाला पाइप आधे समय में टैंक को खाली कर सकता है। तो दूसरा पाइप टैंक को 20 मिनट में खाली कर सकता है।
1 मिनट में दूसरे पाइप द्वारा खाली भाग = 1/20
1 मिनट में दोनों पाइपों द्वारा खाली किया गया भाग = 1/40+1/20
= 1+2/40
= 3/40
तो दो पाइप टैंक को एक साथ 40/3 मिनट = 13 ⅓ मिनट में खाली कर सकते हैं।
अतः सही उत्तर विकल्प B है।
Question 32.
If 5 sec ? – 3 tan ? = 5, then what is the value of 5 tan ? – 3 sec ??
यदि 5 sec x - 3 tan x = 5 है, तो 5 tan x - 3 sec x का मान क्या है?
A.
B.
C.
D.
Answer
C
Explanation
5 sec x-3 tan x = 5
= 5 sec x - 5 = 3 tan x
=5(sec x - 1 ) = 3 tan x
=5[(1/cosx) -1)]=3 tan x
=5(1-cos x)/cos x =3 sin x/cos x
=5(1-cos x) = 3 sin x
=5/3=sin x/(1-cos x)
Multiply and divide by (1+cosx)
=5/3=sin x (1+cos x)/(1-cos x) (1+cos x)
=5/3 = sin x.(1+cos x)/(1-cos^2x)
=5/3=sin x(1+cos x)/sin^2x
=5/3=(1+cos x)/sin x
=5 sin x=3+3cos x
On dividing both sides by cos x .
=5tan x =3sec x + 3
=5tan x - 3 sec x = 3
So the correct answer is option C
5 sec x-3 tan x = 5
= 5 sec x - 5 = 3 tan x
=5(sec x - 1 ) = 3 tan x
=5[(1/cosx) -1)]=3 tan x
=5(1-cos x)/cos x =3 sin x/cos x
=5(1-cos x) = 3 sin x
=5/3=sin x/(1-cos x)
(1 + cosx) गुणा करें और भाग करें
=5/3=sin x (1+cos x)/(1-cos x) (1+cos x)
=5/3 = sin x.(1+cos x)/(1-cos^2x)
=5/3=sin x(1+cos x)/sin^2x
=5/3=(1+cos x)/sin x
=5 sin x=3+3cos x
Cos x द्वारा दोनों पक्षों को भाग करने पर।
= 5tan x = 3sec x + 3
= 5tan x - 3 sec x = 3
इसलिए सही उत्तर विकल्प C है I
Question 33.
At present, the ratio between the ages of Arun and Deepak is 4 : 3. After 6 years, Arun's age will be 26 years. What is the age of Deepak at present ?
वर्तमान में, अरुण और दीपक की आयु का अनुपात 4: 3 है। 6 वर्ष के बाद, अरुण की आयु 26 वर्ष होगी। वर्तमान में दीपक की उम्र क्या है?
A.
B.
C.
D.
Answer
A
Explanation
Let the present age of Arun and Deepak respectively =4x , 3x
After 6 year the age of Arun=4x+6
After 6 years the age of Deepak=3x+6
Given -
4x+6 = 26
4x =20
X = 5
So the present age of Deepak = 3x = 3*5=15 years
So the correct answer is option A.
माना अरुण और दीपक की वर्तमान आयु क्रमशः 4x, 3x है
6 वर्ष के बाद अरुण की आयु = 4x + 6
6 वर्ष के बाद दीपक की आयु = 3x + 6
दिया हुआ -
4x + 6 = 26
4x = 20
x = 5
तो दीपक की वर्तमान आयु = 3x = 3 * 5 = 15 वर्ष
इसलिए सही उत्तर विकल्प A है।
Question 34.
Circumcentre of ?ABC is O. If ?BAC = 75° and ?BCA = 80°, then what is the value (in degrees) of ?OAC?
ΔABC का परिकेन्द्र O है। यदि ∠BAC = 75 ° और ∠BCA = 80 °, तो ∠OAC का मान (डिग्री में) क्या है?
A.
B.
C.
D.
Answer
B
Explanation
O is the circumcenter of ΔABC . Therefore OA = OB = OC =radius of circumcircle.
In ΔABC :-
∠BAC+∠ABC +∠BCA=180°.
75°+∠ABC +80° =180°
∠ABC =180°-155° = 25°.
In ΔOAC:-
OA =OC = radius of circumcircle.
Let ∠OAC = ∠OCA = x°
∠AOC = 2×∠ABC = 2×25° = 50°.
∠OAC + ∠OCA+ ∠AOC = 180°.
x`+ x° + 50° = 180°.
2x° = 180° - 50° = 130°.
x = 130/2 = 65°.
∠OAC = x° =65°
So the correct answer is option B
O, ΔABC के परिवृत्त का केंद्र है। इसलिए OA = OB = OC = परिधि का त्रिज्या।
ΔABC में: -
∠BAC + CABC + =BCA = 180 °।
75 ° + °ABC +80 ° = 180 °
∠ABC = 180 ° -155 ° = 25 °।
:OAC में: -
OA = OC = परिधि की त्रिज्या।
माना OAC = ∠OCA = x °
∠AOC = 2 × CABC = 2 × 25 ° = 50 °।
∠OAC + AOCA + =AOC = 180 °।
x` + x ° + 50 ° = 180 °।
2x ° = 180 ° - 50 ° = 130 °।
x = 130 °/2 = 65 °।
∠OAC = x ° = 65 °
इसलिए सही उत्तर विकल्प B है l
Question 35.
Abhinav scores 80% in physics and 66% in chemistry and the maximum marks of both the papers are 100. what percent does he score in maths which is of 200 marks, if he scores 80% marks in all the three subjects:
अभिनव ने फिजिक्स में 80% और केमिस्ट्री में 66% अंक प्राप्त किये l दोनों पेपरों के अधिकतम अंक 100 हैं। वह गणित में कितने प्रतिशत अंक प्राप्त करता है जो 200 अंकों का है, यदि वह तीनों विषयों में 80% अंक प्राप्त करता है:
A.
B.
C.
D.
Answer
C
Explanation
Abhinav scores 80% in physics out of 100 numbers so his physics numbers = 80
Abhinav scores 66% in chemistry out of 100 number so his chemistry numbers = 66
Let Abhinav score x numbers in maths out of 200.
Total numbers = 100+100+200 = 400
He scores 80% marks in all the three subjects so -
(80+66+x/400)=80/100
146+x = 320
x = 320-146
X = 174
So in math, he got 174 out of 200 so the required percentage -
(174/200)*100
=87%
So the correct answer is option C.
अभिनव ने 100 अंको में से फिसिक्स में 80% अंक प्राप्त किये, इसलिए उसके फिजिक्स के अंक = 80
अभिनव ने 100 में से केमिस्ट्री में 66% स्कोर किए हैं, इसलिए उसके केमिस्ट्री के अंक = 66
माना कि अभिनव ने 200 में से गणित में x अंक हासिल किए l
कुल अंक = 100 + 100 + 200 = 400
वह तीनों विषयों में 80% अंक प्राप्त करता है, इसलिए -
(80+66+x/400)=80/100
146+x = 320
x = 320-146
X = 174
इसलिए गणित में उन्हें 200 में से 174 मिले, अतः आवश्यक प्रतिशत -
(174/200) * 100
= 87%
इसलिए सही उत्तर विकल्प C है।
Question 36.
What percentage of numbers from 1 to 70 have 1 or 9 in the unit's digit?
1 से 70 तक की संख्या का कितने प्रतिशत के इकाई का अंक 1 और 9 है?
A.
B.
C.
D.
Answer
C
Explanation
The numbers from 1 to 70 have 1 or 9 in the unit's digit
= 1, 9, 11, 19, 21, 29, 31, 39, 41, 49, 51, 59, 61 and 69
So there are a total 14 numbers from 1 to 70 that have 1 or 9 in the units digit.
Percentage = (14*100)/70
= 20 %
So the correct answer is option C.
1 से 70 तक की संख्या इकाई के अंक में 1 या 9 है
= 1, 9, 11, 19, 21, 29, 31, 39, 41, 49, 51, 59, 61 और 69
तो 1 से 70 तक कुल 14 संख्याएँ हैं जो इकाइयों के अंक में 1 या 9 हैं।
प्रतिशत = (14 * 100) / 70
= 20%
इसलिए सही उत्तर विकल्प C है।
Question 37.
A can do a work in 15 days and B in 20 days if they work on it together for 4 days then the fraction of the work that is left is?
A एक काम को 15 दिनों में और B 20 दिनों में कर सकता है यदि वे एक साथ 4 दिनों के लिए उस पर काम करते हैं तो शेष कार्य का अंश है ?
A.
B.
C.
D.
Answer
D
Explanation
A can do a work in 15 days. Then -
1-day work of A = 1/15
B can do a work in 20 days. Then -
1-day work of B = 1/20
1 day work of A and B = 1/15 + 1/20 = 4+3/60 = 7/60
4 days work of for A and B = 4*7/60 = 7/15
Hence the fraction of work left = 1-1/15 = 8/15
So the correct answer is option D.
A एक काम को 15 दिनों में कर सकता है। तब -
A का 1 दिन का कार्य = 1/15
B एक काम को 20 दिनों में कर सकता है। तब -
B का 1 दिन का कार्य = 1/20
A और B का 1 दिन का कार्य = 1/15 + 1/20 = 4+3/60 = 7/60
A और B का 4 दिन का कार्य = 4*7/60 = 7/15
अत: शेष कार्य का अंश = 1-1/15 = 8/15
इसलिए सही उत्तर विकल्प D है।
Question 38.
If 75% of a number is added to 75, then the result is the number itself. The number is :
यदि किसी संख्या का 75%, 75 में जोड़ा जाता है, तो परिणाम स्वयं संख्या है। संख्या है:
A.
B.
C.
D.
Answer
C
Explanation
Let the number be x,
According to the question -
75% of x + 75 = x
= x - 75x/100 =75
= x = 300
So the correct answer is option C.
माना संख्या = x
प्रश्न के अनुसार -
x का 75% + 75 = x
= x - 75x/100 =75
= x = 300
इसलिए सही उत्तर विकल्प C है।
Question 39.
A solid sphere of diameter 17.5 cm is cut into two equal halves. What will be the increase (in cm2 ) in the total surface area?
व्यास 17.5 सेमी के एक ठोस गोले को दो बराबर हिस्सों में काट दिया जाता है। कुल सतह क्षेत्र में वृद्धि (सेमी 2 में) क्या होगी?
A.
B.
C.
D.
Answer
C
Explanation
The diameter of sphere=17.5 cm
The radius of sphere=17.5/2 cm
The surface area of sphere=4 π r^2
The total area of two hemisphere=2*3 π r^2
The increase in the total surface area-
=2*3 π r^2 - 4 π r^2
=2π r^2
=2*22/7 *(17.5/2)^2
=481.25 cm^2
So the correct answer is option C.
गोले का व्यास = 17.5 सेमी
गोले की त्रिज्या = 17.5 / 2 सेमी
गोले का सतह क्षेत्रफल = 4 π r^2
दो गोलार्द्ध का कुल क्षेत्रफल = 2 * 3 π r ^ 2
कुल सतह क्षेत्र में वृद्धि-
=2*3 π r^2 - 4 π r^2
=2π r^2
=2*22/7 *(17.5/2)^2
=481.25 cm^2
इसलिए सही उत्तर विकल्प C है।
Question 40.
An agent gets a commission of 2.5% on the sales of cloth. If on a certain day, he gets Rs. 12.50 as commission, the cloth sold through him on that day is worth
एक एजेंट को कपड़े की बिक्री पर 2.5% का कमीशन मिलता है। यदि किसी निश्चित दिन पर, वह 12.50 रु कमीशन के रूप में प्राप्त करता है , उस दिन उसके माध्यम से बेचा गया कपड़ा मूल्य है l
A.
B.
C.
D.
Answer
B
Explanation
Let the total sale = x rs
Then -
2.5%. of x = 12.50
= [ 25/10 * 1/100) * x = 125/10
= x = 500
So the correct answer is option B.
माना कुल बिक्री = x रु
तब -
x का 2.5% = 12.50
= [ 25/10 * 1/100) * x = 125/10
= x = 500
इसलिए सही उत्तर विकल्प B है।
Reasoning Ability
Question 1.
In each of the following question, select the related number from the given alternatives.
7 : 17 :: ? : 50
निम्नलिखित प्रत्येक प्रश्न में, दिए गए विकल्पों में से संबंधित संख्या का चयन करें।
7 : 17 :: ? : 50
A.
B.
C.
D.
Answer
A
Explanation
Relationship between 7:17-
2^3-1=8-1=7
4^2+1=16+1
Similarly the relationship between ?:50-
5^3-1=125-1=124
7^2+1=49+1=50
So the missing number is 124.
Hence the correct answer is option A.
7:17 के बीच संबंध-
2^3-1=8-1=7
4^2+1=16+1
इसी प्रकार ?:50 के बीच संबंध -
5^3-1=125-1=124
7^2+1=49+1=50
लुप्त संख्या 124 है।
अतः सही उत्तर विकल्प A है।
Question 2.
Choose the correct alternative from the given ones that will complete the series.
7 : 48 : : 11 : ?
दिए गए विकल्पों में से सही विकल्प चुनें जो श्रृंखला को पूरा करेगा।
7: 48:: 11:?
A.
B.
C.
D.
Answer
A
Explanation
7 : 48 : : 11 : ?
7 x 7 -1 = 48
11 x 11 -1 = 120
So the correct answer is option A.
7 : 48 : : 11 : ?
7 x 7 -1 = 48
11 x 11 -1 = 120
इसलिए सही उत्तर विकल्प A है।
Question 3.
A cube is made by folding the given sheet. In the cube so formed, what would be the symbol on the opposite side of the # symbol?
दी गई शीट को मोड़कर एक घन बनाया जाता है। इस प्रकार बने घन में # चिन्ह के विपरीत दिशा में कौन सा चिन्ह होगा?
A.
B.
C.
D.
Answer
C
Explanation
& would be the symbol on the opposite side of the # symbol.
So the correct answer is option C.
You can see the solution in the below image -
# चिन्ह के विपरीत दिशा में & चिन्ह होगा
इसलिए सही उत्तर विकल्प C है।
इसका समाधान आप नीचे इमेज में देख सकते हैं -
Question 4.
Find the missing (?) in the series.
Smoke : Pollution : : Fire : ?
श्रंखला में लुप्त (?) ज्ञात करे l
धुआं: प्रदूषण:: आग:?
A.
B.
C.
D.
Answer
C
Explanation
Smoke : Pollution : : Fire :Ash
The pollution is produced from smoke ,the same way the ash is produced from fire.
So the correct answer is option C.
धुआं: प्रदूषण:: आग: राख
प्रदूषण धुएं से उत्पन्न होता है, उसी तरह आग से राख पैदा होती है।
इसलिए सही उत्तर विकल्प C है।
Question 5.
In a certain code language, "MATCH" is written as "NYWYM" and "BOARD" is written as "CMDNI". How is "PRINT" written in that code language?
एक निश्चित कोड भाषा में, MATCH को NYWYM और BOARD को CMDNI के रूप में लिखा जाता है। उस कोड भाषा में PRINT कैसे लिखा जाता है?
A.
B.
C.
D.
Answer
D
Explanation
QPLJY
Refer to the image for the solution -
QPLJY
समाधान के लिए चित्र देखें -
Question 6.
What is the next number?
474, 459, 429, 369, 249, ?
अगली संख्या क्या है ?
474, 459, 429, 369, 249,?
A.
B.
C.
D.
Answer
A
Explanation
474-459=15
459-429 =30
429- 369= 60
369- 249= 120
249-9=240
So the correct answer is option A.
474-459=15
459-429 =30
429- 369= 60
369- 249= 120
249-9=240
इसलिए सही उत्तर विकल्प A है।
Question 7.
If 27 * 4 = 77 and 31 * 9 = 239, then 21 * 6 = ?
यदि 27 * 4 = 77 और 31 * 9 = 239, तो 21 * 6 =?
A.
B.
C.
D.
Answer
C
Explanation
27 * 4 = 77
27(4-1) x 4=77
31 * 9 = 239
31(9-1) x 9=239
21 * 6 =?
21(6-1) x 6=99
So the correct answer is option C.
27 * 4 = 77
27(4-1) x 4=77
31 * 9 = 239
31(9-1) x 9=239
21 * 6 =?
21(6-1) x 6=99
इसलिए सही उत्तर विकल्प C है।
Question 8.
Select the correct combination of mathematical signs that can sequentially replace the * signs and balance the given equation.
42 * 7 * 64 * 11 * 6 *4
गणितीय चिह्नों के उस सही संयोजन का चयन करें जो *चिह्नों को क्रमिक रूप से बदल सके और दिए गए समीकरण को संतुलित कर सके।
42*7*64*11*6*4
A.
B.
C.
D.
Answer
C
Explanation
Put all the options in the given equation.
On putting Option 1.
42 ÷ 7 - 64 + 11 x 6 = 4
6 - 64 + 66 = 4
6 + 2 = 4
8 = 4
Not Correct.
On putting Option 2.
42 x 7 + 64 - 11 ÷ 6 = 4
294+64- 1.8 = 4
Not Correct.
On putting Option 3.
42 ÷ 7 + 64 - 11 x 6 = 4
6 + 64 - 66 = 4
6-2 = 4
4=4
Correct.
Hence option C replaces the * signs and balances the given equation.
So the correct answer is option C.
दिए गए समीकरण में सभी विकल्पों को रखें।
विकल्प 1 को रखने पर -
42 7 - 64 + 11 x 6 = 4
6 - 64 + 66 = 4
6 + 2 = 4
8 = 4
सही नहीं है l
विकल्प 2 को रखने पर -
42 x 7 + 64 - 11 6 = 4
294+64- 1.8 = 4
सही नहीं है l
विकल्प 3 को रखने पर -
42 7 + 64 - 11 x 6 = 4
6 + 64 - 66 = 4
6-2 = 4
4=4
सही है l
अत: विकल्प C, * चिन्हों को प्रतिस्थापित करता है और दिए गए समीकरण को संतुलित करता है।
इसलिए सही उत्तर विकल्प C है।
Question 9.
If 'S' is written as 'H' 'R' as '@' 'A' as '^' 'M' as '#', 'T' as '$' and 'E' as '%' then this code How will 'MASTER' be written in ?
यदि ‘S’ को ‘H’ लिखा जाए ‘R’ को ‘@’ ‘A’ को ‘^’ ‘M’ को ‘#’, ‘T’ को ‘$’ और ‘E’ को ‘%’ तो इस कोड में ‘MASTER’ को कैसे लिखा जायेगा ?
A.
B.
C.
D.
Answer
A
Explanation
S = H
R = @
A = ^
M = #
T = $
E = %
Hence MASTER = #^H$%@
So the correct answer is option A.
S = H
R = @
A = ^
M = #
T = $
E = %
अतः MASTER = #^H$%@
इसलिए सही उत्तर विकल्प A है l
Question 10.
In a certain code language, "CASIO" is written as "3119915". How is "CITIZEN" written in that code language?
एक निश्चित कोड भाषा में, "CASIO" को "3119915" लिखा जाता है। उस कोड भाषा में "CITIZEN" कैसे लिखा जाता है?
A.
B.
C.
D.
Answer
D
Explanation
C=3 A =1 S =18 I =9 O=15
C =3 I =9 T =20 I =9 Z =26 E =5 N =14
So the correct answer is option D.
C=3 A =1 S =18 I =9 O=15
C =3 I =9 T =20 I =9 Z =26 E =5 N =14
इसलिए सही उत्तर विकल्प D है।
Question 11.
In the following question, select the missing number from the given series.
2, 5, 12, 27, ?
निम्नलिखित प्रश्न में दिए गए विकल्पों में से लुप्त अंक ज्ञात कीजिये |
2, 5, 12, 27,?
A.
B.
C.
D.
Answer
D
Explanation
2, 5, 12, 27, ?
2*2+1=5
5*2+2=12
12*2+3=27
27*2+4=58
So the correct answer is option D.
2, 5, 12, 27, ?
2*2+1=5
5*2+2=12
12*2+3=27
27*2+4=58
इसलिए सही उत्तर विकल्प A है।
Question 12.
Which number should come next in the series 48, 24, 12, ......?
श्रंखला 48, 24, 12, ...... में आगे कौन सी संख्या आनी चाहिए?
A.
B.
C.
D.
Answer
B
Explanation
48, 24, 12....?
In the above series, each number is one-half of its previous number.
So we can easily get the next number by dividing the previous number by 2.
48/2 = 24
24/2 = 12
12/2 = 6
Hence 6 will be the next number of the given series.
So the correct answer is option B.
48, 24, 12....
उपरोक्त श्रृंखला में, प्रत्येक संख्या अपनी पिछली संख्या का आधा है।
तो हम पिछली संख्या को 2 से विभाजित करके आसानी से अगली संख्या प्राप्त कर सकते हैं।
48/2 = 24
24/2 = 12
12/2 = 6
अत: 6 दी गई श्रंखला की अगली संख्या होगी।
इसलिए सही उत्तर विकल्प B है।
Question 13.
In the following question, select the missing number from the given series.
1, 6, 13, 22, 33, ?
निम्नलिखित प्रश्न में दिए गए विकल्पों में से लुप्त अंक ज्ञात कीजिये |
1, 6, 13, 22, 33,?
A.
B.
C.
D.
Answer
D
Explanation
6−1=5
13−6=7
22−13=9
33−22=11
46−33=13
So the correct answer is option D.
6−1=5
13−6=7
22−13=9
33−22=11
46−33=13
इसलिए सही उत्तर विकल्प D है।
Question 14.
In this question, select the related word from the given alternatives.
GHI : DFH : : LMN : ?
इस प्रश्न में, दिए गए विकल्पों में से संबंधित शब्द का चयन करें।
GHI: DFH:: LMN:?
A.
B.
C.
D.
Answer
D
Explanation
G H I
+5+5+5
L M N
D F H
+5+5+5
I K M
So the correct answer is option D.
G H I
+5+5+5
L M N
D F H
+5+5+5
I K M
इसलिए सही उत्तर विकल्प D है।
Question 15.
A series is given with one term missing. Select the correct alternative from the given ones that will complete the series.
19, 38, ?, 228, 684, 1368
एक श्रृंखला लुप्त संख्या के साथ दी गई है। दिए गए विकल्पों में से सही विकल्प का चयन करें जो श्रृंखला को पूरा करेगा l
19, 38, ?, 228, 684, 1368
A.
B.
C.
D.
Answer
C
Explanation
19, 38, ?, 228, 684, 1368
19 x 2=38
114 x 2=228
684 x 2=1368
So the correct answer is option C.
19, 38, ?, 228, 684, 1368
19 x 2=38
114 x 2=228
684 x 2=1368
इसलिए सही उत्तर विकल्प C है।
Question 16.
King :throne::rider:?
राजा :सिंहासन::सवार:?
A.
B.
C.
D.
Answer
C
Explanation
As the king sits on the throne, similarly the rider sits on the saddle placed on the horse's back.
Hence the correct answer is option C.
जिस प्रकार राजा सिंहासन पर बैठता है उसी प्रकार सवार घोड़े की पीठ पर रखी काठी पर बैठता है l
अतः सही उत्तर विकल्प C है l
Question 17.
In the following question, select the related word from the given alternatives.
HMPU : IOSY : : GMRF : ?
निम्नलिखित प्रश्न में, दिए गए विकल्पों में से संबंधित शब्द का चयन करें।
HMPU : IOSY : : GMRF : ?
A.
B.
C.
D.
Answer
B
Explanation
H M P U
+1+2+3+4
I O S Y
G M R F
+1+2+3+4
H O U J
So the correct answer is option B
H M P U
+1+2+3+4
I O S Y
G M R F
+1+2+3+4
H O U J
इसलिए सही उत्तर विकल्प B है।
Question 18.
In the following number series only one number is wrong. Find out the wrong number.
1, 125, 729, 2177
निम्नलिखित संख्या श्रृंखला में केवल एक संख्या गलत है। गलत नंबर का पता लगाएं।
1, 125, 729, 2177
A.
B.
C.
D.
Answer
C
Explanation
1 = 1^3
125 = 5^3
729 = 9^3
2197=13^3
So 2177 is wrong. There will be 2197 in the place of 2177.
So the correct answer is option C.
1 = 1^3
125 = 5^3
729 = 9^3
2197 = 13^3
अतः 2177 गलत है। 2177 के स्थान पर 2197 होगा।
इसलिए सही उत्तर विकल्प C है।
Question 19.
Which letter should come next in the series, Q, J, E, B, _?
श्रृंखला, Q, J, E, B, _ में अगला कौन सा अक्षर आना चाहिए?
A.
B.
C.
D.
Answer
B
Explanation
Q, J, E, B, _?
In this series, the consecutive prime number is decreased in order.
Q-7 = J
J-5 = E
E-3 = B
B-2 = Z (2 is the smallest prime number.)
Hence the next letter will be Z.
So the correct answer is option B.
इस श्रृंखला में क्रमागत अभाज्य संख्याएँ क्रम से घट रही हैं।
Q-7 = J
J-5 = E
E-3 = B
B-2 = Z (2 सबसे छोटी अभाज्य संख्या है।)
अतः अगला अक्षर Z होगा।
इसलिए सही उत्तर विकल्प B है।
Question 20.
Below the statement is given two arguments numbered I and II. Considering the statement and the arguments given next to it, you have to decide which element is/is stronger in them.
Statement:
Should it be compulsory to have a job after school?
Argument:
l. Yes, it helps in developing life skills.
ll. No, not all students are fully mature in dealing with work matters.
नीचे कथन के आगे I और II दो तर्क दिए हुए है l आपको कथन एवं उसके आगे दिए गए तर्कों पर विचार करते हुए यह निर्णय लेना है कि उनमें कौन सा तत्व मजबूत है/हैं l
कथन:
क्या स्कूल के बाद काम (जॉब) करना अनिवार्य होना चाहिए?
तर्क:
l. हाँ, इससे जीवन कौशल विकसित करने में मदद मिलती है l
ll. नहीं सभी छात्र कार्य में आने वाले मामलों को निपटाने में पूरी तरह से परिपक्व नहीं होते है l
A.
B.
C.
D.
Answer
D
Explanation
According to Statement I, having a job after school helps in developing life skills. This argument is justified. But it is also true that not all students are fully mature to deal with work matters.
So both the arguments are strong.
So the correct answer is option D.
कथन I के अनुसार स्कूल के बाद काम (जॉब) करने से जीवन कौशल विकसित करने में मदद मिलती है l यह तर्कउचित है l परन्तु यह भी उचित है कि सभी छात्र कार्य में आने वाले मामलों को निपटाने में पूरी तरह से परिपक्व नहीं होते है l
अतः दोनों ही तर्क मजबूत है l
इसलिए सही उत्तर विकल्प D है l
Question 21.
Which of the following pair is is NOT correctly matched?
निम्नलिखित में से कौन सी जोड़ी सही ढंग से मेल नहीं खाती है?
A.
B.
C.
D.
Answer
D
Explanation
Ozone layer is not related to Troposphere.
So the correct answer is option D.
ओजोन परत ट्रोपोस्फीयर से संबंधित नहीं है।
इसलिए सही उत्तर विकल्प D है।
Question 22.
In each of the following questions, find the odd number/letters/word from the given alternatives
निम्नलिखित प्रश्न में, दिए गए विकल्पों में से विषम संख्या / अक्षर / शब्द ज्ञात कीजिए
A.
B.
C.
D.
Answer
C
Explanation
Bridge is different from other because the meaning of Ladder , Staircase and Escalator is same.
So the correct answer is option C.
Bridge अन्य से अलग है क्योंकि Ladder, Staircase और Escalator का अर्थ समान होता है।
इसलिए सही उत्तर विकल्प C है।
Question 23.
In the given question, select the related letter from the given alternatives.
DBCE:QOPR::JLKI:?
दिए गए प्रश्न में दिए गए विकल्पों में से संबंधित अक्षर को चुनिए।
DBCE:QOPR::JLKI:?
A.
B.
C.
D.
Answer
C
Explanation
D(4)+13=17(Q)
B(2)+13=15(O)
C(3)+13=16(P)
E(5)+13=18(R)
Similarly in JLKI:?
J(10)+13=W(23)
L(12)+13=Y(25)
K(11)+13=X(24)
I(9)+13=V(22)
So the related letters are WYXV.
Hence the correct answer is option C.
D(4)+13=17(Q)
B(2)+13=15(O)
C(3)+13=16(P)
E(5)+13=18(R)
इसी तरह JLKI:? में
J(10)+13=W(23)
L(12)+13=Y(25)
K(11)+13=X(24)
I(9)+13=V(22)
संबंधित अक्षर WYXV हैं।
अतः सही उत्तर विकल्प C है।
Question 24.
Choose the correct alternative from the given ones that will complete the series.
6, 9 , 15, 24, 39, 63, ?
दिए गए विकल्पों में से सही विकल्प चुनें जो श्रृंखला को पूरा करेगा।
6, 9, 15, 24, 39, 63,?
A.
B.
C.
D.
Answer
C
Explanation
6, 9 , 15, 24, 39, 63, ?
6+9=15 15+9=24 24+15=39 24+39=63 39+63=102
So the correct answer is option C.
6, 9 , 15, 24, 39, 63, ?
6+9=15 15+9=24 24+15=39 24+39=63 39+63=102
इसलिए सही उत्तर विकल्प C है।
Question 25.
In the given question, select the related number from the given alternatives.
17 : ? : : 145 : 195
दिए गए प्रश्न में, दिए गए विकल्पों में से संबंधित संख्या का चयन करें।
17 : ? : : 145 : 195
A.
B.
C.
D.
Answer
B
Explanation
The relationship between 145:195
145=144+1=12^2+1
195=196-1=14^2-1
Similarly the relationship between 17:?-
17=16+1=4^2+1
25=36-1=6^2-1
So the related number is 35.
Hence the correct answer is option B.
145:195 के बीच संबंध -
145=144+1=12^2+1
195=196-1=14^2-1
इसी प्रकार 17:? के बीच संबंध -
17=16+1=4^2+1
35=36-1=6^2-1
संबंधित संख्या 35 है।
अतः सही उत्तर विकल्प B है।
Question 26.
Replace the question mark with an option that follows the same logic applied in the first pair 4232:11::1291: ??
प्रश्न चिह्न को एक विकल्प से बदलें जो पहली जोड़ी में लागू किए गए उसी तर्क का अनुसरण करता है l
4232: 11 :: 1291: ??
A.
B.
C.
D.
Answer
D
Explanation
4+2+3+2=11
1+2+9+1=13
So the correct answer is option D.
4+2+3+2=11
1+2+9+1=13
इसलिए सही उत्तर विकल्प D है।
Question 27.
Select the related word/letters/number from the given alternatives.
600: 2000:: ?:9000
दिए गए विकल्पों में से सम्बंधित शब्द/अक्षर/संख्या को चुनिए l
600: 2000:: ?:9000
A.
B.
C.
D.
Answer
B
Explanation
20*30=600
40*50=2000
70*80=5600
90*100=9000
So the missing term is 5600.
Hence the correct answer is option B.
20*30=600
40*50=2000
70*80=5600
90*100=9000
विलुप्त पद 5600 है l
अतः सही उत्तर विकल्प B है l
Question 28.
In a certain code language, "CAGES" is written as "NADYB" and "SILVER" is written as "LZRIGR". How is "WATER" written in that code language?
एक निश्चित कोड भाषा में, "CAGES" को "NADYB" के रूप में लिखा जाता है और "SILVER" को "LZRIGR" के रूप में लिखा जाता है। उस कोड भाषा में "WATER" कैसे लिखा जायेगा ?
A.
B.
C.
D.
Answer
A
Explanation
MAQYV
Refer to the image for the solution -
MAQYV
समाधान के लिए चित्र को देखे -
Question 29.
Select the correct option that indicates the arrangement of the given words in the order in which they appear in an English dictionary.
1. Freeze
2. Freedom
3. Fryer
4. Frozen
5. Fraud
6. Fringe
सही विकल्प का चयन करें जो दिए गए शब्दों की व्यवस्था को उसी क्रम में इंगित करता है जिस क्रम में वे अंग्रेजी शब्दकोश में दिखाई देते हैं।
1. Freeze
2. Freedom
3. Fryer
4. Frozen
5. Fraud
6. Fringe
A.
B.
C.
D.
Answer
D
Explanation
The correct arrangement is -
5. Fraud
2. Freedom
1. Freeze
6. Fringe
4. Frozen
3. Fryer
Option D is the correct arrangement of the given words in the order in which they appear in an English dictionary.
So the correct answer is option D.
सही व्यवस्था है -
5. Fraud
2. Freedom
1. Freeze
6. Fringe
4. Frozen
3. Fryer
विकल्प D दिए गए शब्दों का अंग्रेजी शब्दकोश में आने के क्रम में सही व्यवस्था है।
इसलिए सही उत्तर विकल्प D है।
Question 30.
A word is represented by only one set of numbers as given in one of the alternatives. Two classes of the alphabet represent the sets of numbers given in the alternatives as in the two matrices given below. The number of columns and rows of Matrix-I is 0 to 4 and of Matrix-II is numbered from 5 to 9. From these matrices, a letter can be represented first by its row and then by the column number. For example, F can be represented by 30, 22 etc. N can be represented by 97, 89 etc. Similarly you have to identify the set for the given word.
‘DAKU’
एक शब्द केवल एक संख्या-समूह द्वारा दर्शाया गया है, जैसा कि विकल्पों में से किसी एक में दिया गया है। विकल्पों में दिए गए संख्या-समूह अक्षरों के दो वर्गों द्वारा दर्शाएं गए हैं, जैसा कि दिए गए दो आव्यूहों में है। आव्यूह-I के स्तम्भ और पंक्ति की संख्या 0 से 4 है और आव्यूह-II के स्तम्भ और पंक्ति की संख्या 5 से 9 है। इन आव्यूहों से एक अक्षर को पहले उसकी पंक्ति और बाद में स्तम्भ संख्या द्वारा दर्शाया जा सकता है। उदाहरण के लिए F को 30, 22 आदि द्वारा दर्शाया जा सकता है l N को 97, 89 आदि द्वारा दर्शाया जा सकता है l इसी तरह से आपको दिए गए शब्द के लिए समूह को पहचानना है l
‘DAKU’
A.
B.
C.
D.
Answer
D
Explanation
The group given in option D is correct for the word 'DAKU'.
So the correct answer is option D.
‘DAKU’ शब्द के लिए विकल्प D में दिया गया समूह सही है l
इसलिए सही उत्तर विकल्प D है l
Question 31.
If 'P 3 Q' means 'P is daughter of Q', 'P 5 Q' means 'P is father of Q', 'P 7 Q' means 'P is mother of Q' and 'P 9 Q' means 'P is sister of Q', then how is J related to K in J 3 L 9 N 3 O 5 K?
यदि 'P 3 Q' का अर्थ 'P, Q की पुत्री है', 'P 5 Q' का अर्थ है 'P, Q का पिता है', 'P 7 Q' का अर्थ है 'P, Q की माता है' और 'P 9 Q' का अर्थ है ' P, Q की बहन है, तो J 3 L 9 N 3 O 5 K में J, K से कैसे संबंधित है?
A.
B.
C.
D.
Answer
D
Explanation
J 3 L 9 N 3 O 5 K
J 3 L = J is daughter of L
L 9 N = L is sister of N
N 3 O = N is daughter of O
O 5 K = O is father of K
L and N are sisters and K is also brother/sister of L and N. J is daughter of L so J is Niece of K.
So the correct answer is option D.
J 3 L 9 N 3 O 5 K
J 3 L = J, L की बेटी है
L 9 N = L, N की बहन है
N 3 O = N, O की बेटी है
O 5 K = O, K का पिता है
L और N बहनें हैं और K, L और N का भाई / बहन है l J, L की बेटी है इसलिए J, K की भतीजी है।
इसलिए सही उत्तर विकल्प D है।
Question 32.
If in a certain language, MADRAS is coded as NBESBT, how is BOMBAY coded in that code ?
यदि किसी निश्चित भाषा में, MADRAS को NBESBT के रूप में कोडित किया जाता है, तो BOMBAY को उस कोड में कैसे कोडित किया जाता है?
A.
B.
C.
D.
Answer
B
Explanation
MADRAS = NBESBT
M=N
A=B
D=E
S=T
R=S
A=B
S=T
So-
BOMBAY=?
B=C
O=P
M=N
B=C
A=B
Y=Z
BOMBAY=CPNCBZ
So the correct answer is option B.
MADRAS = NBESBT
M=N
A=B
D=E
S=T
R=S
A=B
S=T
अतः -
BOMBAY=?
B=C
O=P
M=N
B=C
A=B
Y=Z
BOMBAY=CPNCBZ
इसलिए सही उत्तर विकल्प B है।
Question 33.
A series is given with one term missing. Select the correct alternative from the given ones that will complete the series
BD, CE, DF, EG, ?
एक श्रृंखला लुप्त पद के साथ दी गई है। दिए गए विकल्पों में से सही विकल्प का चयन करें जो श्रृंखला को पूरा करेगा
BD, CE, DF, EG,?
A.
B.
C.
D.
Answer
C
Explanation
B C D E F(no are increasing by +1)
D E F G H
So the correct answer is option C.
B C D E F(+1 की वृद्धि हो रही है I)
D E F G H
इसलिए सही उत्तर विकल्प C है।
Question 34.
In a row of boys, Amrith is seventh from the left and Amar is twelfth from the right. If they interchange their positions, Amrith becomes 22nd from the left. How many boys are there in the row?
लड़कों की एक पंक्ति में, अमृत बाएं से सातवें और अमर दाएं से बारहवें स्थान पर है। यदि वे अपने स्थान को बदल देते हैं, तो अमृत बाईं ओर से 22 वें स्थान पर आ जाता है। पंक्ति में कितने लड़के हैं?
A.
B.
C.
D.
Answer
C
Explanation
Amrith is seventh from the left and Amar is twelfth from the right. If they interchange their positions, Amrith becomes 22nd from the left.
Now there are 21 students on the left of Amrith and 11 students on the right of Amrith.
So the total number of students = 21+Amrith+11
= 21+1+11 = 33
So there are 33 students in the class.
So the correct answer is option C.
अमृथ बाईं ओर से सातवें और अमर दाहिने से बारहवें हैं। यदि वे अपने स्थान को बदल देते हैं, तो अमृथ बाईं ओर से 22 वें स्थान पर हो जाता है।
अब अमृथ के बाईं ओर 21 छात्र और दाईं ओर 11 छात्र हैं।
तो छात्रों की कुल संख्या = 21 + अमृत + 11
= 21 + 1 + 11 = 33
अतः कक्षा में 33 छात्र हैं।
इसलिए सही उत्तर विकल्प C है।
Question 35.
In this question, select the related word from the given alternatives.
12 : 39 :: 15 : ?
इस प्रश्न में, दिए गए विकल्पों में से संबंधित शब्द का चयन करें।
12: 39 :: 15:?
A.
B.
C.
D.
Answer
A
Explanation
12 x 3 + 3=39
15 x 3 + 3=48
So the correct answer is option A.
12 x 3 + 3=39
15 x 3 + 3=48
इसलिए सही उत्तर विकल्प A है।
Question 36.
Choose the correct alternative from the given ones that will complete the series.
4, 9, 16, 25, 36, ?
दिए गए विकल्पों में से सही विकल्प चुनें जो श्रृंखला को पूरा करेगा।
4, 9, 16, 25, 36, ?
A.
B.
C.
D.
Answer
A
Explanation
4=(2)^2
9=(3)^2
16=(4)^2
25=(5)^2
36=(7)^2
49=(7)^2
So the correct answer is option A.
4=(2)^2
9=(3)^2
16=(4)^2
25=(5)^2
36=(7)^2
49=(7)^2
इसलिए सही उत्तर विकल्प A है।
Question 37.
If 38+15 = 66 and 29+36 = 99, then 82+44 = ?
यदि 38+15 = 66 और 29+36 = 99 हो, तो 82+44 = ?
A.
B.
C.
D.
Answer
C
Explanation
In the first equation - 38+15 = 66 (3+8) * (1+6) = 11*6 = 66 In the second equation - 29+36 = 99 (2+9) * (3+6) = 11*9 = 99 Similarly - 82+44 =? (8+2) * (4+4) = 10*8 = 80 Hence 82+44 = 80 So the correct answer is option C.
पहले समीकरण में - 38+15 = 66 (3+8) * (1+6) = 11*6 = 66 दूसरे समीकरण में - 29+36 = 99 (2+9) * (3+6) = 11*9 = 99 इसी प्रकार - 82+44 =? (8+2) * (4+4) = 10*8 = 80 अतः 82+44 = 80 इसलिए सही उत्तर विकल्प C है।
Question 38.
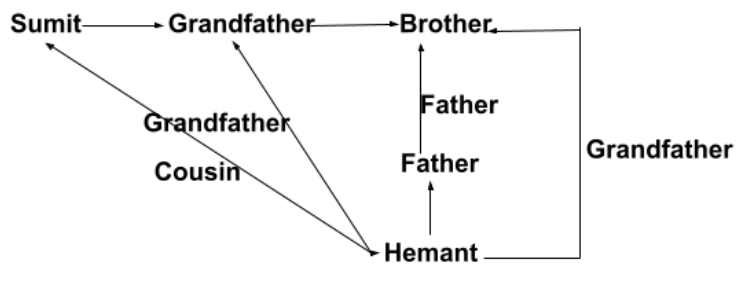
Sumit's grandfather's brother is the father of Hemant's father. How is Sumit related to Hemant?
सुमित के दादा का भाई, हेमंत के पिता का पिता है। सुमित, हेमंत से कैसे सम्बंधित है ?
A.
B.
C.
D.
Answer
B
Explanation
The brother of Sumit's grandfather is Hemant's grandfather. Hence Sumit's grandfather and Hemant's grandfather is brother. Hence both Sumit and Hemant are cousins.
So the correct answer is option B.
सुमित के दादा का भाई, हेमंत का दादा है। अतः सुमित का दादा और हेमंत का दादा भाई है। अतः सुमित और हेमंत दोनों चचेरे भाई है।
इसलिए सही उत्तर विकल्प B है।
Question 39.
Look at this series: 12, 11, 13, 12, 14, 13, … What number should come next?
इस श्रृंखला को देखें: 12, 11, 13, 12, 14, 13,… आगे कौन सी संख्या आनी चाहिए?
A.
B.
C.
D.
Answer
D
Explanation
You can see the solution the below image -
आप नीचे दिए गए चित्र में समाधान देख सकते है -
Question 40.
A man walks 5 kilometre towards South and then turns to the right. After walking 3 kilometre, he turns to the left and walks 5 kilometre. Now in which direction is he from the starting point?
एक आदमी 5 किलोमीटर दक्षिण की ओर चलता है और फिर दाईं ओर मुड़ता है। 3 किलोमीटर चलने के बाद, वह बाईं ओर मुड़ता है और 5 किलोमीटर चलता है। अब वह प्रारंभिक बिंदु से किस दिशा में है?
